摘要:1 2 3 4 5 6 7 8 9 10 11 12 D D A D A C D B C D B B 13 14 15 16 17 18 19 20 21 22 23 24 A C B D D C A D D A B C
网址:http://m.1010jiajiao.com/timu_id_3999868[举报]
给定数列1,2+3+4,5+6+7+8+9,10+11+12+13+14 +15+16,…,则这个数列的一个通项公式是
[ ]
A.an=2n2+3n-1
B.an=n2+5n-5
C.an=2n3-3n2+3n-1
D.an=2n3-n2+n-2
查看习题详情和答案>>
B.an=n2+5n-5
C.an=2n3-3n2+3n-1
D.an=2n3-n2+n-2
判断题:
(1)
两个长度相等的向量一定相等;[
](2)
相等的向量起点必相同;[
](3)
平行向量就是共线向量;[
](4)
若向量a的模小于b的模,则a<b;[
](5)
质量、动量、功、加速度都是向量;[
](6)
[
](7)
向量a与b平行,则a与b的方向相同或相反;[
](8)
在△ABC中, ;
;
[
](9)
若向量a与b有共同的起点,则以b的终点为起点,以a的终点为终点的向量等于b-a;[
](10)
若 且b≠0,当a=
且b≠0,当a= 时,则一定有a,b共线;
时,则一定有a,b共线;
[
](11)
若a·b=0,则 或
或 ;
;
[
](12)
若a·b=a·c,且a≠0,则b=c;[
](13)
向量a在b方向上的射影是一个模等于 (
( 是a与b的夹角),方向与b相同或相反的向量;
是a与b的夹角),方向与b相同或相反的向量;
[ ]
(14) .
.
[
] 查看习题详情和答案>>设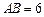 ,在线段
,在线段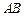 上任取两点C,D(端点
上任取两点C,D(端点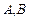 除外),将线段
除外),将线段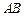 分成三条线段AC,CD,DB.
分成三条线段AC,CD,DB.
(1)若分成的三条线段的长度均为正整数,求这三条线段可以构成三角形(称事件A)的概率;
(2)若分成的三条线段的长度均为正实数,求这三条线段可以构成三角形(称事件B)的概率;
(3)根据以下用计算机所产生的20组随机数,试用随机数摸拟的方法,来近似计算(Ⅱ)中事件B的概率.
20组随机数如下:
| | 1组 | 2组 | 3组 | 4组 | 5组 | 6组 | 7组 | 8组 | 9组 | 10组 |
| X | 0.52 | 0.36 | 0.58 | 0.73 | 0.41 | 0. 6 6 | 0.05 | 0.32 | 0.38 | 0.73 |
| Y | 0.76 | 0.39 | 0.37 | 0.01 | 0.04 | 0.28 | 0.03 | 0.15 | 0.14 | 0 .86 .86 |
| | 11组 | 12组 | 13组 | 14组 | 15组 | 16组 | 17组 | 18组 | 19组 | 20组 |
| X | 0.67 | 0.47 | 0.58 | 0.21 | 0.54 | 0. 64 64 | 0.36 | 0.35 | 0.95 | 0.14 |
| Y | 0.41 | 0.54 | 0.51 | 0.37 | 0.31 | 0.23 | 0.56 | 0.89 | 0.17 | 0.03 |
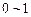 之间的均匀随机数,Y也是
之间的均匀随机数,Y也是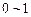 之间的均匀随机
之间的均匀随机 数)
查看习题详情和答案>>
数)
查看习题详情和答案>>
设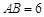 ,在线段
,在线段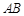 上任取两点C,D(端点
上任取两点C,D(端点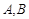 除外),将线段
除外),将线段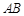 分成三条线段AC,CD,DB.
分成三条线段AC,CD,DB.
(1)若分成的三条线段的长度均为正整数,求这三条线段可以构成三角形(称事件A)的概率;
(2)若分成的三条线段的长度均为正实数,求这三条线段可以构成三角形(称事件B)的概率;
(3)根据以下用计算机所产生的20组随机数,试用随机数摸拟的方法,来近似计算(Ⅱ)中事件B的概率.
20组随机数如下:
|
|
1组 |
2组 |
3组 |
4组 |
5组 |
6组 |
7组 |
8组 |
9组 |
10组 |
|
X |
0.52 |
0.36 |
0.58 |
0.73 |
0.41 |
0. 6 |
0.05 |
0.32 |
0.38 |
0.73 |
|
Y |
0.76 |
0.39 |
0.37 |
0.01 |
0.04 |
0.28 |
0.03 |
0.15 |
0.14 |
0.86 |
|
|
11组 |
12组 |
13组 |
14组 |
15组 |
16组 |
17组 |
18组 |
19组 |
20组 |
|
X |
0.67 |
0.47 |
0.58 |
0.21 |
0.54 |
0. 64 |
0.36 |
0.35 |
0.95 |
0.14 |
|
Y |
0.41 |
0.54 |
0.51 |
0.37 |
0.31 |
0.23 |
0.56 |
0.89 |
0.17 |
0.03 |
(X是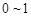 之间的均匀随机数,Y也是
之间的均匀随机数,Y也是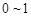 之间的均匀随机数)
之间的均匀随机数)
查看习题详情和答案>>
设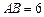 ,在线段
,在线段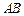 上任取两点C,D(端点
上任取两点C,D(端点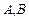 除外),将线段
除外),将线段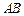 分成三条线段AC,CD,DB.
分成三条线段AC,CD,DB.
(1)若分成的三条线段的长度均为正整数,求这三条线段可以构成三角形(称事件A)的概率;
(2)若分成的三条线段的长度均为正实数,求这三条线段可以构成三角形(称事件B)的概率;
(3)根据以下用计算机所产生的20组随机数,试用随机数摸拟的方法,来近似计算(Ⅱ)中事件B的概率.
20组随机数如下:
(X是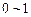 之间的均匀随机数,Y也是
之间的均匀随机数,Y也是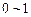 之间的均匀随机
之间的均匀随机 数)
数)
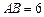 ,在线段
,在线段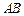 上任取两点C,D(端点
上任取两点C,D(端点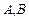 除外),将线段
除外),将线段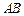 分成三条线段AC,CD,DB.
分成三条线段AC,CD,DB.(1)若分成的三条线段的长度均为正整数,求这三条线段可以构成三角形(称事件A)的概率;
(2)若分成的三条线段的长度均为正实数,求这三条线段可以构成三角形(称事件B)的概率;
(3)根据以下用计算机所产生的20组随机数,试用随机数摸拟的方法,来近似计算(Ⅱ)中事件B的概率.
20组随机数如下:
| | 1组 | 2组 | 3组 | 4组 | 5组 | 6组 | 7组 | 8组 | 9组 | 10组 |
| X | 0.52 | 0.36 | 0.58 | 0.73 | 0.41 | 0. 6 6 | 0.05 | 0.32 | 0.38 | 0.73 |
| Y | 0.76 | 0.39 | 0.37 | 0.01 | 0.04 | 0.28 | 0.03 | 0.15 | 0.14 | 0 .86 .86 |
| | 11组 | 12组 | 13组 | 14组 | 15组 | 16组 | 17组 | 18组 | 19组 | 20组 |
| X | 0.67 | 0.47 | 0.58 | 0.21 | 0.54 | 0. 64 64 | 0.36 | 0.35 | 0.95 | 0.14 |
| Y | 0.41 | 0.54 | 0.51 | 0.37 | 0.31 | 0.23 | 0.56 | 0.89 | 0.17 | 0.03 |
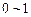 之间的均匀随机数,Y也是
之间的均匀随机数,Y也是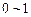 之间的均匀随机
之间的均匀随机 数)
数)