摘要:设(2-x)100=a0+a1x+a2x2+-+a100x100.求下列各式的值: (1)a0; (2)a1+a2+-+a100; (3)a1+a3+a5+-+a99; (4)(a0+a2+-+a100)2-(a1+a3+-+a99)2. 解 (1)由(2-x)100展开式中的常数项为C·2100, 即a0=2100.或令x=0.则展开式可化为a0=2100. (2)令x=1,可得 a0+a1+a2+-+a100=(2-)100. ① ∴a1+a2+-+a100=(2-)100-2100. (3)令x=-1可得 a0-a1+a2-a3+-+a100=(2+)100. ② 与x=1所得到的①联立相减可得. a1+a3+-+a99=. (4)原式=[(a0+a2+-+a100)+(a1+a3+-+a99)]×[(a0+a2+-+a100)-(a1+a3+-+a99)] =(a0+a1+a2+-+a100)(a0-a1+a2-a3+-+a98-a99+a100) =(2-)100·(2+)100=1.
网址:http://m.1010jiajiao.com/timu_id_3995753[举报]
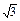 x)100=a0+a1x+a2x2+…+a100x100,求下列各式的值:
x)100=a0+a1x+a2x2+…+a100x100,求下列各式的值: