摘要:3.通过对分段定义函数.复合函数.抽象函数等的认识.进一步体会函数关系的本质.进一步树立运动变化.相互联系.制约的函数思想.为函数思想的广泛运用打好基础. 本部分的难点首先在于克服“函数就是解析式 的片面认识.真正明确不仅函数的对应法则.而且其定义域都包含着对函数关系的制约作用.并真正以此作为处理问题的指导.其次在于确定函数三要素.求反函数等课题的综合性.不仅要用到解方程.解不等式等知识.还要用到换元思想.方程思想等与函数有关概念的结合. Ⅰ 深化对函数概念的认识 例1.下列函数中.不存在反函数的是 ( ) 分析:处理本题有多种思路.分别求所给各函数的反函数.看是否存在是不好的.因为过程太繁琐. 从概念看.这里应判断对于给出函数值域内的任意值.依据相应的对应法则.是否在其定义域内都只有惟一确定的值与之对应.因此可作出给定函数的图象.用数形结合法作判断.这是常用方法. 此题作为选择题还可采用估算的方法.对于D.y=3是其值域内一个值.但若y=3.则可能x=2.也可能x=-1.依据概念.则易得出D中函数不存在反函数.于是决定本题选D. 说明:不论采取什么思路.理解和运用函数与其反函数的关系是这里解决问题的关键. 由于函数三要素在函数概念中的重要地位.那么掌握确定函数三要素的基本方法当然成了函数概念复习中的重要课题. 例1.函数的定义域是( D ) A. B. C. D. 例2.函数()的反函数是( D ) A. B. C. D. 也有个别小题的难度较大.如 例3.函数其中P.M为实数集R的两个非空子集.又规定..给出下列四个判断: ①若.则 ②若.则 ③若.则 ④若.则 其中正确判断有( B ) A. 1个 B. 2个 C. 3个 D. 4个 分析:若.则只有这一种可能.②和④是正确的. Ⅱ 系统小结确定函数三要素的基本类型与常用方法
网址:http://m.1010jiajiao.com/timu_id_3994067[举报]
已知函数f(x)=
(a为非零常数),定义:f1(x)=f(x),fk+1(x)=f[fk(x)],k∈N*,例如:f2(x)=f[f(x)],f3(x)=f[f2(x)],…
(1)当a=2时,求f2(1),f3(-
)的值;
(2)若对于任意x≠-1,等式f2(x)=x恒成立,求a的值;
(3)当a确定后,fk(x),k∈N*的值都由x的值确定.当a=2时,试通过对fk(x)的探究,写出一个使得集合{fk(x)}为有限集的真命题(不必证明).
查看习题详情和答案>>
| ax |
| x+1 |
(1)当a=2时,求f2(1),f3(-
| 1 |
| 7 |
(2)若对于任意x≠-1,等式f2(x)=x恒成立,求a的值;
(3)当a确定后,fk(x),k∈N*的值都由x的值确定.当a=2时,试通过对fk(x)的探究,写出一个使得集合{fk(x)}为有限集的真命题(不必证明).
已知函数f(x)=
(a为非零常数),定义:f1(x)=f(x),fk+1(x)=f[fk(x)],k∈N*,例如:f2(x)=f[f(x)],f3(x)=f[f2(x)],…
(1)当a=2时,求f2(1),f3(-
)的值;
(2)若对于任意x≠-1,等式f2(x)=x恒成立,求a的值;
(3)当a确定后,fk(x),k∈N*的值都由x的值确定.当a=2时,试通过对fk(x)的探究,写出一个使得集合{fk(x)}为有限集的真命题(不必证明).
查看习题详情和答案>>
| ax |
| x+1 |
(1)当a=2时,求f2(1),f3(-
| 1 |
| 7 |
(2)若对于任意x≠-1,等式f2(x)=x恒成立,求a的值;
(3)当a确定后,fk(x),k∈N*的值都由x的值确定.当a=2时,试通过对fk(x)的探究,写出一个使得集合{fk(x)}为有限集的真命题(不必证明).
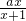 (a为非零常数),定义:f1(x)=f(x),fk+1(x)=f[fk(x)],k∈N*,例如:f2(x)=f[f(x)],f3(x)=f[f2(x)],…
(a为非零常数),定义:f1(x)=f(x),fk+1(x)=f[fk(x)],k∈N*,例如:f2(x)=f[f(x)],f3(x)=f[f2(x)],…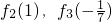 的值;
的值; 对任意函数f(x),x∈D,可按如图构造一个数列发生器,记由数列发生器产生数列{xn}.
对任意函数f(x),x∈D,可按如图构造一个数列发生器,记由数列发生器产生数列{xn}.