摘要:利用向量可以解决线段相等.直线垂直.立体几何中空间角(异面直线的角.线面角.二面角)和空间距离(点线距.线线距.线面距.面面距).建立坐标系.写出坐标.可以“以数定形 . 例10.如图所示.P是正方形的ABCD的对角线BD上一点.四边形PECF是矩形. 求证:(1).PA=EF (2).PA⊥EF 建立如图的坐标系.设正方形的边长是1.︱︱=, 则A(0,1),P(,),E(,0),F(1, ) ∴=(-,1-) =(-1,- ) (1).∵︱︱=(-)+(1-) =-+1 ︱︱=(-1)+ (-) =-+1 ∴︱︱=︱︱.即PA=EF (2). ﹡=(-)(-1)+(1-)(-) =--++=0 ∴⊥.即PA⊥EF 例11.如图所示.在棱长为1的正方形ABCD-ABCD中.E,F分别是DD,BD的中点.G在棱CD上.且CG=CD,H是CG的中点. ⑴.求证:EF⊥BC ⑵.求证:EF与C G所成角的余弦值 ⑶.求FH的长 解:如图所示.建立空间直角坐标系D-xyz. E(0,0, ) F(,,0) C B G(0, ,0) (1).证明: =(,,-) = ∵·=·(-1)+ ·0+·(-1)=0 ∴⊥ ∴EF⊥BC (2). =(0,- ,-1) ∴∣∣== 由(1)得 ∣∣= ·= ∴cos== (3). ∵H是C G的中点 ∴H(,,)即H(0..) 又∵F(,,0) ∴FH=︱︱== 点评:利用空间向量解决立体几何问题.将抽象的逻辑论证转化为代数计算.以数助形.大大降低了空间想象能力.是数形结合的深化.
网址:http://m.1010jiajiao.com/timu_id_3993618[举报]
下列三个说法不正确的个数是
①零向量是长度为0的向量,所以零向量与非零向量不平行.
②因为平面内的向量与这个平面内的有向线段一一对应,所以平面内的向量可以用这个平面内的有向线段表示.
③因为向量
∥
,所以AB∥CD.( )
①零向量是长度为0的向量,所以零向量与非零向量不平行.
②因为平面内的向量与这个平面内的有向线段一一对应,所以平面内的向量可以用这个平面内的有向线段表示.
③因为向量
| AB |
| CD |
| A、3 | B、2 | C、1 | D、0 |
 如图1:等边
如图1:等边 可以看作由等边
可以看作由等边 绕顶点
绕顶点 经过旋转相似变换得到.但是我们注意到图形中的
经过旋转相似变换得到.但是我们注意到图形中的 和
和 的关系,上述变换也可以理解为图形是由
的关系,上述变换也可以理解为图形是由 绕顶点
绕顶点 旋转
旋转 形成的.于是我们得到一个结论:如果两个正三角形存在着公共顶点,则该图形可以看成是由一个三角形绕着该顶点旋转
形成的.于是我们得到一个结论:如果两个正三角形存在着公共顶点,则该图形可以看成是由一个三角形绕着该顶点旋转 形成的.
形成的.
① 利用上述结论解决问题:如图2, 中,
中, 都是等边三角形,求四边形
都是等边三角形,求四边形 的面积;
的面积;
② 图3中,  ∽
∽ ,
, ,仿照上述结论,推广出符合图3的结论.(写出结论即可)
,仿照上述结论,推广出符合图3的结论.(写出结论即可)
如图1:等边 可以看作由等边
可以看作由等边 绕顶点
绕顶点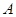 经过旋转相似变换得到.但是我们注意到图形中的
经过旋转相似变换得到.但是我们注意到图形中的 和
和 的关系,上述变换也可以理解为图形是由
的关系,上述变换也可以理解为图形是由 绕顶点
绕顶点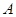 旋转
旋转 形成的.于是我们得到一个结论:如果两个正三角形存在着公共顶点,则该图形可以看成是由一个三角形绕着该顶点旋转
形成的.于是我们得到一个结论:如果两个正三角形存在着公共顶点,则该图形可以看成是由一个三角形绕着该顶点旋转 形成的.
形成的.

① 利用上述结论解决问题:如图2, 中,
中, 都是等边三角形,求四边形
都是等边三角形,求四边形 的面积;
的面积;
② 图3中,  ∽
∽ ,
, ,仿照上述结论,推广出符合图3的结论.(写出结论即可)
,仿照上述结论,推广出符合图3的结论.(写出结论即可)
查看习题详情和答案>>
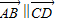 ,所以AB∥CD.( )
,所以AB∥CD.( )