摘要: 已知..求证:. 先完成证明 → 讨论:证明过程有什么特点?
网址:http://m.1010jiajiao.com/timu_id_3992170[举报]
先阅读下列不等式的证法,再解决后面的问题:已知![]() ,
,![]() ,求证
,求证![]() .
.
证明:构造函数![]() ,
,![]()
因为对一切![]() ,恒有
,恒有![]() ≥0,所以
≥0,所以![]() ≤0,从而得
≤0,从而得![]() ,
,
(1)若![]() ,
,![]() ,请写出上述结论的推广式;
,请写出上述结论的推广式;
(2)参考上述解法,对你推广的结论加以证明.
查看习题详情和答案>>
请选做一题,都做时按先做的题判分,都做不加分.
(1)已知向量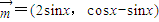 ,
,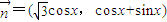 ,函数
,函数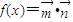 .
.
①求函数f(x)的最小正周期和值域;
②在△ABC中,角A、B、C所对的边分别是a、b、c,若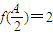 且a2=bc,试判断△ABC的形状.
且a2=bc,试判断△ABC的形状.
(2)已知锐角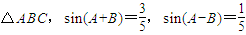 .
.
①求证:tanA=2tanB;
②设AB=3,求AB边上的高CD的长.
查看习题详情和答案>>
(1)已知向量
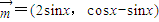 ,
,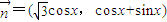 ,函数
,函数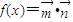 .
.①求函数f(x)的最小正周期和值域;
②在△ABC中,角A、B、C所对的边分别是a、b、c,若
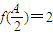 且a2=bc,试判断△ABC的形状.
且a2=bc,试判断△ABC的形状.(2)已知锐角
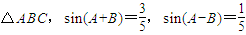 .
.①求证:tanA=2tanB;
②设AB=3,求AB边上的高CD的长.
查看习题详情和答案>>
(本小题15分)
先阅读下列不等式的证法,再解决后面的问题:已知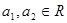 且
且 ,求证
,求证
证明:构造函数 因为对一切
因为对一切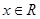 ,恒有
,恒有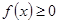 ,所以
,所以 4-8
4-8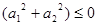 ,从而
,从而
(1)若 ,且
,且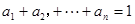 ,请写出上述结论的推广式;
,请写出上述结论的推广式;
(2)参考上述证法,对你的结论加以证明;
(3)若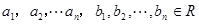 ,求证
,求证
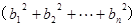
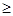
 .[
.[
查看习题详情和答案>>
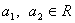 ,
, ,求证
,求证 .
.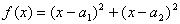 ,
,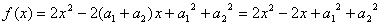
 ,恒有
,恒有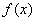 ≥0,所以
≥0,所以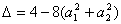 ≤0,从而得
≤0,从而得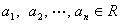 ,
,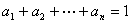 ,请写出上述结论的推广式;
,请写出上述结论的推广式;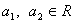 ,
,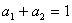 ,求证
,求证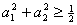 .
.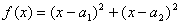 ,
,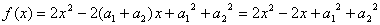
 ,恒有
,恒有 ≥0,所以
≥0,所以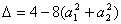 ≤0,从而得
≤0,从而得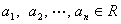 ,
,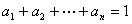 ,请写出上述结论的推广式;
,请写出上述结论的推广式;