摘要：如图所示.设△ABC的外接圆的切线 AE与BC的延长线交于点E.∠BAC的平分线与BC交 于点D. 求证:ED2=EC·EB. 证明 如图所示.因为AE是圆的切线. 所以∠ABC=∠CAE. 又因为AD是∠BAC的平分线.所以∠BAD=∠CAD. 从而∠ABC+∠BAD=∠CAE+∠CAD. 因为∠ADE=∠ABC+∠BAD. ∠DAE=∠CAE+∠CAD. 所以∠ADE=∠DAE.故EA=ED. 因为EA是圆的切线.所以由切割线定理知. EA2=EC·EB. 而EA=ED.所以ED2=EC·EB.
网址：http://m.1010jiajiao.com/timu_id_3990843[举报]
中，以
轴为始边做两个锐角
，它们的终边分别与单位圆相交于A，B两点，已知A，B的横坐标分别为
的值； （2） 求
的值。
（2008•江苏二模）如图，平面直角坐标系xOy中，△AOB和△COD为两等腰直角三角形，A（-2，0），C（a，0）（a＞0）．设△AOB和△COD的外接圆圆心分别为M，N．（1）若⊙M与直线CD相切，求直线CD的方程；
（2）若直线AB截⊙N所得弦长为4，求⊙N的标准方程；
（3）是否存在这样的⊙N，使得⊙N上有且只有三个点到直线AB的距离为
| 2 |
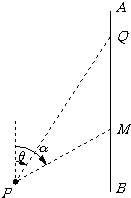（2008•江苏二模）如图，AB是沿太湖南北方向道路，P为太湖中观光岛屿，Q为停车场，PQ=5.2km．某旅游团游览完岛屿后，乘游船回停车场Q，已知游船以13km/h的速度沿方位角θ的方向行驶，sinθ=| 5 |
| 13 |
（Ⅰ）设sinα=
| 4 |
| 5 |
（Ⅱ）设小船速度为10km/h，请你替该游客设计小船行驶的方位角α，当角α余弦值的大小是多少时，游客甲能按计划以最短时间到达Q．