摘要:感应电动势计算:. ε=BLv
网址:http://m.1010jiajiao.com/timu_id_3989401[举报]
 桌面上放着一个单匝矩线圈,线圈中心上方一定高度上有一竖立的条形磁体(如图),此时线圈内的磁通量为0.04Wb.把条形磁体竖放在线圈内的桌面上时,线圈的磁通量为0.12Wb,分别计算以下两个过程中线圈中的感应电动势.
桌面上放着一个单匝矩线圈,线圈中心上方一定高度上有一竖立的条形磁体(如图),此时线圈内的磁通量为0.04Wb.把条形磁体竖放在线圈内的桌面上时,线圈的磁通量为0.12Wb,分别计算以下两个过程中线圈中的感应电动势.(1)把条形磁体从图中位置在0.5s内放到线圈内的桌面上.
(2)换用100匝的矩形线圈,线圈面积和原单匝线圈相同,把条形磁体从图中位置在0.1s内放到线圈内的桌面上.
 如图所示,桌面上放一个单匝线圈,线圈中心上方一定高度上有一竖立的条形磁铁,此时线圈内的磁通量为0.02Wb,把条形磁铁竖放在线圈内的桌面上时,线圈内磁通量为0.12Wb.分别计算以下两个过程中线圈中感应电动势.
如图所示,桌面上放一个单匝线圈,线圈中心上方一定高度上有一竖立的条形磁铁,此时线圈内的磁通量为0.02Wb,把条形磁铁竖放在线圈内的桌面上时,线圈内磁通量为0.12Wb.分别计算以下两个过程中线圈中感应电动势.(1)把条形磁铁从图中位置在0.2s内放到线圈内的桌面上,产生感应电动势
(2)换用5匝的矩形线圈,线圈面积和原单匝线圈相同,把条形磁铁从图中位置在0.5s内放到线圈内的桌面上.
 如图甲所示是利用涡流冶炼金属的感应炉示意图,冶炼炉内装入被冶炼的金属,线圈通上高频交变电流,这时被冶炼的金属中就产生很强的涡流,从而产生大量的热使金属熔化,这种冶炼方法速度快,温度容易控制,并能避免有害杂质混入被冶炼的金属中,因此适于冶炼特种合金和特种钢,其简化模型如图乙所示.假设金属环的阻值R=10πΩ,半径r=10cm,其外侧线圈中通以高频的交流电,线圈中产生垂直于金属环所在平面的变化磁场,磁场的磁感应强度B随时间变化关系为B=0.1sin(4×104t)(T).不计温度变化对电阻的影响,计算结果可保留π.求:
如图甲所示是利用涡流冶炼金属的感应炉示意图,冶炼炉内装入被冶炼的金属,线圈通上高频交变电流,这时被冶炼的金属中就产生很强的涡流,从而产生大量的热使金属熔化,这种冶炼方法速度快,温度容易控制,并能避免有害杂质混入被冶炼的金属中,因此适于冶炼特种合金和特种钢,其简化模型如图乙所示.假设金属环的阻值R=10πΩ,半径r=10cm,其外侧线圈中通以高频的交流电,线圈中产生垂直于金属环所在平面的变化磁场,磁场的磁感应强度B随时间变化关系为B=0.1sin(4×104t)(T).不计温度变化对电阻的影响,计算结果可保留π.求:(1)金属环中产生的感应电动势最大值;
(2)1s时间内金属环内产生的焦耳热;
(3)在磁场变化的0时刻到四分之一周期时间内,通过金属环截面的电荷量. 查看习题详情和答案>>
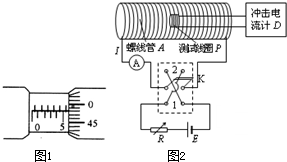 (1)在“利用单摆测重力加速度”的实验中,测得单摆的摆角小于5°,完成n次全振动的时间为t,用毫米刻度尺测得的摆线长为L,用螺旋测微器测得摆球的直径为d.
(1)在“利用单摆测重力加速度”的实验中,测得单摆的摆角小于5°,完成n次全振动的时间为t,用毫米刻度尺测得的摆线长为L,用螺旋测微器测得摆球的直径为d.①用上述物理量的符号写出求重力加速度的一般表达式g=
4π2n2(L+
| ||
| t2 |
4π2n2(L+
| ||
| t2 |
②从图1可知,摆球直径d的读数为
5.980
5.980
.③实验中有个同学发现他测得的重力加速度的值总是偏大,其原因可能是下述原因中的
BC
BC
.A、悬点未固定紧,振动中出现松动,使摆线增长了
B、把n次全振动的时间误作为(n+1)次全振动的时间
C、以摆线长作为摆长来计算
(2)如图2所示是测量通电螺线管A内部磁感应强度B及其与电流I关系的实验装置.将截面积为S、匝数为N的小试测线圈P置于螺线管A中间,试测线圈平面与螺线管的轴线垂直,可认为穿过该试测线圈的磁场均匀.将试测线圈引线的两端与冲击电流计D相连.拨动双刀双掷换向开关K,改变通入螺线管的电流方向,而不改变电流大小,在P中产生的感应电流引起D的指针偏转.
| 实验次数 | I(A) | B(×10-3T) |
| 1 | 0.5 | 0.62 |
| 2 | 1.0 | 1.25 |
| 3 | 1.5 | 1.88 |
| 4 | 2.0 | 2.51 |
| 5 | 2.5 | 3.12 |
| dm |
| N△? |
| dm |
| 2NDΦS |
| dm |
| 2NDΦS |
| dm |
| D?△t |
| dm |
| D?△t |
②调节可变电阻R,多次改变电流并拨动K,得到A中电流I和磁感应强度B的数据,见右表.由此可得,螺线管A内部在感应强度B和电流I的关系为B=
0.00125I
0.00125I
.③为了减小实验误差,提高测量的准确性,可采取的措施有
AB
AB
A.适当增加试测线圈的匝数N B.适当增大试测线圈的横截面积S
C.适当增大可变电阻R的阻值 D.适当拨长拨动开关的时间△t.
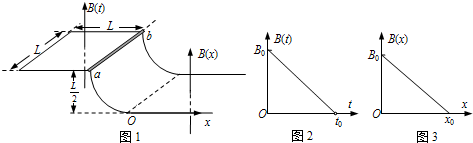
如图1所示,一端封闭的两条平行光滑长导轨相距L,距左端L处的右侧一段被弯成半径为
的四分之一圆弧,圆弧导轨的左、右两段处于高度相差
的水平面上.以弧形导轨的末端点O为坐标原点,水平向右为x轴正方向,建立Ox坐标轴.圆弧导轨所在区域无磁场;左段区域存在空间上均匀分布,但随时间t均匀变化的磁场B(t),如图2所示;右段区域存在磁感应强度大小不随时间变化,只沿x方向均匀变化的磁场B(x),如图3所示;磁场B(t)和B(x)的方向均竖直向上.在圆弧导轨最上端,放置一质量为m的金属棒ab,与导轨左段形成闭合回路,金属棒由静止开始下滑时左段磁场B(t)开始变化,金属棒与导轨始终接触良好,经过时间t0金属棒恰好滑到圆弧导轨底端.已知金属棒在回路中的电阻为R,导轨电阻不计,重力加速度为g.
(1)求金属棒在圆弧轨道上滑动过程中,回路中产生的感应电动势E;
(2)如果根据已知条件,金属棒能离开右段磁场B(x)区域,离开时的速度为v,求金属棒从开始滑动到离开右段磁场过程中产生的焦耳热Q;
(3)如果根据已知条件,金属棒滑行到x=x1位置时停下来,
a.求金属棒在水平轨道上滑动过程中通过导体棒的电荷量q;
b.通过计算,确定金属棒在全部运动过程中感应电流最大时的位置.
查看习题详情和答案>>
| L |
| 2 |
| L |
| 2 |
(1)求金属棒在圆弧轨道上滑动过程中,回路中产生的感应电动势E;
(2)如果根据已知条件,金属棒能离开右段磁场B(x)区域,离开时的速度为v,求金属棒从开始滑动到离开右段磁场过程中产生的焦耳热Q;
(3)如果根据已知条件,金属棒滑行到x=x1位置时停下来,
a.求金属棒在水平轨道上滑动过程中通过导体棒的电荷量q;
b.通过计算,确定金属棒在全部运动过程中感应电流最大时的位置.
