摘要:已知为坐标原点,点F.T.M.P分别满足. (1) 当t 变化时,求点P的轨迹方程; (2) 若的顶点在点P的轨迹上,且点A的纵坐标,的重心恰好为点F, 求直线BC的方程.
网址:http://m.1010jiajiao.com/timu_id_3987546[举报]
(本小题满分14分)
已知抛物线、椭圆、双曲线都经过点M(1,2),它们在x轴上有共同焦点,椭圆和双曲线的对称轴是坐标轴,抛物线的顶点为坐标原点。
(Ⅰ)求这三条曲线方程;
(Ⅱ)若定点P(3,0),A为抛物线上任意一点,是否存在垂直于x轴的直线l被以AP为直径的圆截得的弦长为定值?若存在,求出l的方程;若不存在,说明理由。
查看习题详情和答案>>(本小题满分14分) 已知在单位圆x²+y²=1上任取一点M,作MN⊥x轴,垂足为N,  = 2
= 2 .
.
(Ⅰ)求动点Q的轨迹 的方程;
的方程;
(Ⅱ)设点 ,点
,点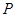 为曲线
为曲线 上任一点,求点
上任一点,求点 到点
到点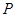 距离的最大值
距离的最大值 ;
;
(Ⅲ)在 的条件下,设△
的条件下,设△ 的面积为
的面积为 (
( 是坐标原点,
是坐标原点,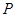 是曲线
是曲线 上横坐标为
上横坐标为 的点),以
的点),以 为边长的正方形的面积为
为边长的正方形的面积为 .若正数
.若正数 满足
满足 ,问
,问 是否存在最小值,若存在,请求出此最小值,若不存在,请说明理由.
是否存在最小值,若存在,请求出此最小值,若不存在,请说明理由.
(本小题满分14分)
已知二次函数 的图象经过坐标原点,与
的图象经过坐标原点,与 轴的另一个交点为
轴的另一个交点为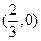 ,且
,且 ,数列
,数列 的前
的前 项的和为
项的和为 ,点
,点 在函数
在函数 的图象上.
的图象上.
(1)求函数 的解析式;
的解析式;
(2)求数列 的通项公式;
的通项公式;
(3)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
 = 2
= 2 .
. 的方程;
的方程; ,点
,点 为曲线
为曲线 到点
到点 ;
; 的条件下,设△
的条件下,设△ 的面积为
的面积为 (
( 是坐标原点,
是坐标原点, 的点),以
的点),以 .若正数
.若正数 满足
满足 ,问
,问
 ,其左准线为
,其左准线为 ,右准线为
,右准线为 ,抛物线
,抛物线 以坐标原点
以坐标原点 为顶点,
为顶点, 两点.
两点. 的长度.
的长度.