摘要：命题:①单调递减的无穷数列不存在极限,②常数列的极限是这个常数本身,③摇摆的无穷数列不存在极限.以上命题正确的是( ) A.0 B.1 C.2 D.3 答案:B.由极限的定义仅有②是正确的.①的反例是an=这是无穷单调递减数列.它的极限是零,③的反例是an=它是摇摆的无穷数列.它的极限是零.因为|an-0|=|-0|=可以任意小.故选B.
网址：http://m.1010jiajiao.com/timu_id_3987295[举报]
已知三个命题：①关于x的方程x2+mx+2m=0无实数根；②关于x的不等式|x+2|+|x-3|＞m对于任意的x∈R恒成立；③函数f(x)=
在[-2，0）上单调递减．如果上述三个命题中两真一假，那么实数m的取值范围是（ ）
| x2+m2 |
| x |
查看习题详情和答案>>
已知三个命题：①关于x的方程x2+mx+2m=0无实数根；②关于x的不等式|x+2|+|x-3|＞m对于任意的x∈R恒成立；③函数f(x)=
在[-2，0）上单调递减．如果上述三个命题中两真一假，那么实数m的取值范围是（ ）
查看习题详情和答案>>
| x2+m2 |
| x |
| A．（-2，0）∪（2，8） | B．（-2，0]∪（5，8）∪[9，+∞） |
| C．（-∞，-2）∪（5，8） | D．（-∞，-2]∪（0，2）∪[5，8） |
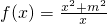在[-2，0）上单调递减．如果上述三个命题中两真一假，那么实数m的取值范围是