摘要：5．关于函数f(x)=lg(x≠0.x∈R).有下列命题: ①函数y=f(x)的图象关于y轴对称, ②当x＞0时.f(x)是增函数,当x＜0时.f(x)是减函数, ③函数f(x)的最小值是lg2, ④当-1＜x＜0或x＞1时.f((x)是增函数． 其中正确的命题的序号是 (把你认为正确命题的序号都填上) [典型例题]: 例1．已知.1)比较与的大小, 2)若0＜a＜b..求证:ab＜1 例2．已知过原点O的一条直线与函数的图象交于A.B二点.分别过点A.B作y轴的平行线与函数图象交于C.D二点. 1)证明:点C.D和原点在同一直线上, 2)当BC平行x轴时.求点A的坐标, 例3．定义在R上的单调函数f(x)满足且对任意x.y∈R都有 f求证f(x)为奇函数, (2)若f(k·3)+f(3-9-2)＜0对任意x∈R恒成立.求实数k的取值范围． 例4．已知是定义在上的奇函数.且.若...有,(1)判断函数在上的单调性.并证明你的结论, (2) ⑵解不等式 (3)若≤对所有的.恒成立.求实数的取值范围. [命题展望]:
网址：http://m.1010jiajiao.com/timu_id_3986225[举报]
关于函数f(x)＝lg
(x≠0，x∈R)有下列命题：
①函数y＝f(x)的图像关于y轴对称；
②当x＞0时f(x)是增函数，当x＜0时f(x)是减函数；
③函数f(x)的最小值是lg2；
④当x＞1时f(x)没有反函数．
其中正确命题的序号是________(注：把你认为正确的序号都填上)
查看习题详情和答案>>下列命题中：
①f（x）的图象与f（-x）关于y轴对称．
②f（x）的图象与-f（-x）的图象关于原点对称．
③y=|lgx|与y=lg|x|的定义域相同，它们都只有一个零点．
④二次函数f（x）满足f（2-x）=f（2+x）并且有最小值，则f（0）＜f（5）．
⑤若定义在R上的奇函数f（x），有f（3+x）=-f（x），则f（2010）=0
其中所有正确命题的序号是
查看习题详情和答案>>
①f（x）的图象与f（-x）关于y轴对称．
②f（x）的图象与-f（-x）的图象关于原点对称．
③y=|lgx|与y=lg|x|的定义域相同，它们都只有一个零点．
④二次函数f（x）满足f（2-x）=f（2+x）并且有最小值，则f（0）＜f（5）．
⑤若定义在R上的奇函数f（x），有f（3+x）=-f（x），则f（2010）=0
其中所有正确命题的序号是
①②④⑤
①②④⑤
．下列命题中：
（1）方程x2+（a-3）x+a=0有一个正实根，一个负实根，则a＜0；
（2）函数f（x）=lg（mx2+mx+1）的定义域为R，则m的取值范围是m∈（0，4）；
（3）若函数y=
在区间（-∞，1]上是减函数，则实数a∈[-3，-2]；
（4）若函数f（3x+1）是偶函数，则f（x）的图象关于直线x=
对称．
（5）若对于任意x∈（1，3）不等式x2-ax+2＜0恒成立，则a＞
；
其中的真命题是
查看习题详情和答案>>
（1）方程x2+（a-3）x+a=0有一个正实根，一个负实根，则a＜0；
（2）函数f（x）=lg（mx2+mx+1）的定义域为R，则m的取值范围是m∈（0，4）；
（3）若函数y=
| x2+ax+2 |
（4）若函数f（3x+1）是偶函数，则f（x）的图象关于直线x=
| 1 |
| 3 |
（5）若对于任意x∈（1，3）不等式x2-ax+2＜0恒成立，则a＞
| 11 |
| 3 |
其中的真命题是
（1），（3），（5）
（1），（3），（5）
（写出所有真命题的编号）．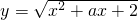
在区间（-∞，1]上是减函数，则实数a∈[-3，-2]；
对称．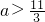
；