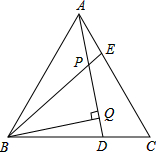
摘要： (1)∵△ABC为等腰三角形 ∴AC=BC ∠CAB=∠CBA 又∵CH为底边上的高.P为高线上的点 ∴PA=PB ∴∠PAB=∠PBA ∵∠CAE=∠CAB-∠PAB ∠CBF=∠CBA-∠PBA ∴∠CAE=∠CBF (2)∵AC=BC ∠CAE=∠CBF ∠ACE=∠BCF ∴△ACE-△BCF(AAS) ∴AE=BF (3)若存在点P能使S△ABC=S△ABG.因为AE=BF.所以△ABG也是一个等腰三角形.这两个三角形面积相等.底边也相同.所以高也相等.进而可以说明△ABC-△ABG.则对应边AC=AE,∠ACE=∠AEC,所以0°≤∠C＜90°
网址：http://m.1010jiajiao.com/timu_id_3982547[举报]
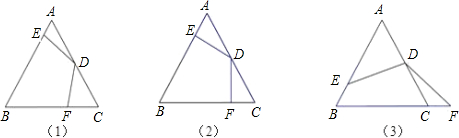
已知△ABC为等边三角形，D为AC的中点，∠EDF=120°，DE交线段AB于E，DF交直线BC于F．
（1）如图（1），求证：DE=DF；
（2）如图（2），若BE=3AE，求证：CF=
BC．
（3）如图（3），若BE=
AE，则CF= BC；在图（1）中，若BE=4AE，则CF= BC．
查看习题详情和答案>>
（1）如图（1），求证：DE=DF；
（2）如图（2），若BE=3AE，求证：CF=
| 1 |
| 4 |
（3）如图（3），若BE=
| 1 |
| 3 |
查看习题详情和答案>>
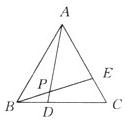22、如图，△ABC为等边三角形，D、E分别是BC、AC上的一点，且BD=CE，AD和BE交于点P，求∠APE的度数．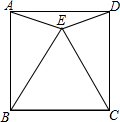
已知，如图，△ABC为等边三角形，AE=CD，AD、BE相交于点P．
如图，△ABC为等边三角形，边长为1．△BCD是顶角为∠BDC且∠BDC=120°的等腰三角形．以D为顶点作一个60°的角，角的两边分别交AB，AC于M，N，延长AC至E点，使CE=BM，连接DE．