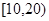摘要:设G是的重心.. (Ⅰ)试用表示,(Ⅱ)试用表示 解:(Ⅰ) ----------------------------------, (Ⅱ) ----------------------------------- 已知函数 (Ⅰ)求证: 在区间内单调递减,在内单调递增, (Ⅱ)求在区间上的最小值. (Ⅰ)证明:设 且.则 又 区间内单调递减,同理可证在内单调递增,----------------------- , (Ⅱ)利用单调性的定义或奇函数的性质可知在区间上单增. ----------------------------------------------------------------------------- 已知 (Ⅰ)求的值, (Ⅱ)求的值. 已知 图象的一部分如图所示: (1)求的解析式,(2)写出的单调区间. 舒城县某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时.可全部租出.当每辆车的月租金每增加50元时.未租出的车将会增加一辆.租出的车每辆每月需要维护费150元.未租出的车每辆每月需要维护费50元. (1)当每辆车的月租金定为3600元时.能租出多少辆车? (2)当每辆车的月租金定为多少元时.租赁公司的月收益最大?最大月收益是多少? 解:(1)当每辆车的月租金定为3600时.未租出的车辆数为:.所以这时租出了88辆车.--------------------------------------------------------------------------------------------------------------- , (2)设每辆本的月租金定为元.则租赁公司的月收益为:. 整理得:.所以.当时.最大.其最大值为.即当每辆车的月租金定为4050元时.租赁公司的月收益最大.最大收益为307050元.--------------------------------------------------------------------------------------------------- , 已知: 是定义在上的函数.且①.②对.恒有 ③时.有 (Ⅰ)求证:=2, (Ⅱ)求证:在上单调递增. (Ⅲ)若.求的取值范围.(提示:注意利用已证结论)
网址:http://m.1010jiajiao.com/timu_id_3981078[举报]
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
(17)(本小题满分12分)
已知函数 .
.
(I)求函数 的最小正周期;
的最小正周期;
(Ⅱ)当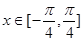 时,函数
时,函数 的最小值为
的最小值为 ,求实数
,求实数 的值.
的值.
查看习题详情和答案>>
((本小题满分12分)
编号分别为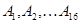 的16名篮球运动员在某次比赛中得分记录如下;
的16名篮球运动员在某次比赛中得分记录如下;
|
编号 |
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
A8 |
|
得分 |
15 |
35 |
21 |
28 |
25 |
36 |
18 |
34 |
|
编号 |
A9 |
A10 |
A11 |
A12 |
A13 |
A14 |
A15 |
A16 |
|
得分 |
17 |
26 |
25 |
33 |
22 |
12 |
31 |
38 |
(Ⅰ)将得分在对应区间的人数填入相应的空格内:
|
区 间 |
|
|
|
|
人 数 |
|
|
|
(Ⅱ)从得分在区间 内的运动员中随机抽取2人.
内的运动员中随机抽取2人.
(1)用运动员编号列出所有可能的抽取结果;
(2)求这两人得分之和大于50的概率.
查看习题详情和答案>>
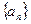 中,
中,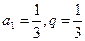 ,
,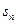 为数列
为数列 项的和,证明:
项的和,证明:
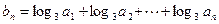 ,求数列
,求数列 的通项公式;
的通项公式;