摘要:几何概型 例3.在平面直角坐标系中.设是横坐标与纵坐标的绝对值均不大于2的点构成的区域.是到原点的距离不大于1的点构成的区域.向中随机投一点.则所投点在中的概率是 分析:本小题考查古典概型.其概率应为几何图形的面积比. 如图:区域D 表示边长为4 的正方形的内部.区域E 表示单位圆及其内部.因此. 答案: 评注:在解决几何概型问题时.要弄清整个事件的区域长度.以及所研究事件的区域长度.特别是平面几何图形的构成常常是考查的焦点.有可能与定积分相联系. 例4.如图所示.墙上挂有一边长为的正方形木板.它的四个角的空白部分都是以正 方形的顶点为圆心.半径为的圆弧.某人向此板投镖.假设每次都能击中木板.且击中木板上每个点的可能性都一样. 则他击中阴影部分的概率是 ( ) A. B. C. D.与的取值有关 分析:本小题考查古典概型.其概率应为几何图形的面积比.其中阴影部分的面积要通过规则的图形的面积求出.即正方形的面积去掉一个圆的面积. 解:正方形的面积为.而四个角空白部分合起来为半径为的一个圆.面积为.所以他击中阴影部分的概率是.故选A. 答案:A 评注:在解决几何概型问题时.对于不规则图形的面积要通过求定积分或规则图形的面积求出. 例5.设有关于的一元二次方程. (Ⅰ)若是从四个数中任取的一个数.是从三个数中任取的一个数.求上述方程有实根的概率. (Ⅱ)若是从区间任取的一个数.是从区间任取的一个数.求上述方程有实根的概率. 分析:一元二次方程有实根的条件为.即.题(Ⅰ)可用列举法列出所有的基本事件.找出符合条件的基本事件.题(Ⅱ)就是几何概型.可作出试验的总区域.和符合条件的区域.应该是把看作有序数对对于平面上的点.可画出平面区域解答. 解:设事件为“方程有实根 . 当.时.方程有实根的充要条件为. (Ⅰ)基本事件共12个: .其中第一个数表示的取值.第二个数表示的取值. 事件中包含9个基本事件.事件发生的概率为. (Ⅱ)试验的全部结束所构成的区域为. 构成事件的区域为. 所以所求的概率为. 评注:本题容纳了古典概型和几何概型的解法.要善于区分提炼.并进行转化.把数组看成平面内的点即可转化为平面区域问题用面积解答.
网址:http://m.1010jiajiao.com/timu_id_3980652[举报]
判断下列概率模型是古典概型还是几何概型?
(1)如图3-3-4,转盘上有8个面积相等的扇形,转动转盘,求转盘停止转动时指针落在阴影部分的概率.
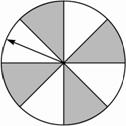
图3-3-4
(2)在500 mL的水中有一个草履虫,现从中随机取出2 mL水样放到显微镜下观察,求发现草履虫的概率.
查看习题详情和答案>>P(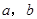 )是平面上的一个点,设事件A表示“
)是平面上的一个点,设事件A表示“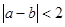 ”,其中
”,其中 为实常数.
为实常数.
(1)若 均为从0,1,2,3,4五个数中任取的一个数,求事件A发生的概率;
均为从0,1,2,3,4五个数中任取的一个数,求事件A发生的概率;
(2)若 均为从区间[0,5)任取的一个数,求事件A发生的概率.
均为从区间[0,5)任取的一个数,求事件A发生的概率.
【解析】本试题考查了几何概型和古典概型结合的一道综合概率计算试题。首先明确区域中的所有基本事件数或者区域表示的面积,然后分别结合概率公式求解得到。
查看习题详情和答案>>
将曲线y=
,x=1,x=2和y=0所围成的平面区域记作d,将直线x=1,x=2,y=0和y=1所围成的正方形区域记作D.
(Ⅰ)在直角坐标平面上,作出区域D和d;
(Ⅱ)利用随机模拟方法,我们可以估算区域d的面积,也就是说,在区域D内随机产生n个点,数出落在区域d内点的个数,用几何概型公式计算区域d的面积.请按此思路,设计一个算法,估算区域d的面积,只要求写出伪代码.
提示:若点(a,b)∈D,则当b<
时,(a,b)∈d.
查看习题详情和答案>>
| 1 |
| x |
(Ⅰ)在直角坐标平面上,作出区域D和d;
(Ⅱ)利用随机模拟方法,我们可以估算区域d的面积,也就是说,在区域D内随机产生n个点,数出落在区域d内点的个数,用几何概型公式计算区域d的面积.请按此思路,设计一个算法,估算区域d的面积,只要求写出伪代码.
提示:若点(a,b)∈D,则当b<
| 1 |
| a |
