摘要：当全部情况为有限种时.也可采用淘汰法. 例18. 已知.则与同时成立的充要条件是 . 解:按实数b的正.负分类讨论. 当b>0时.而等式不可能同时成立, 当b＝0时.无意义, 当b<0时.若a<0.则两不等式不可能同时成立.以上三种情况均被淘汰.故只能为a>0.b<0.容易验证.这确是所要求的充要条件. 跟踪训练: 1已知函数.则 讲解 由.得.应填4.2． 集合的真子集的个数是 讲解 .显然集合M中有90个元素.其真子集的个数是.应填.
网址：http://m.1010jiajiao.com/timu_id_3980622[举报]
某企业为适应市场需求，准备投入资金16万元生产W和R型两种产品．经市场预测，生产W型产品所获利润yW（万元）与投入资金xW（万元）成正比例关系，且当投入资金为6万元时，可获利润1.5 万元．生产R型产品所获利润yR（万元）与投入资金xR（万元）满足关系yR=
．为获得最大总利润，问生产W、R型产品各应投入资金多少万元？获得的最大总利润是多少？
查看习题详情和答案>>
| 1 |
| 2 |
| xR |
某服装店，按每件80元的价格购进一款T恤1000件，根据市场预测，当售价定为100元时，可全部售完．定价每上涨1元，则销售量就会减少5件．定价每下降1元，则销售量就会增加5件．
①当该服装店获得14500元的利润时，售价为多少元？
②当售价定为多少元时，该服装店获得的利润最大？
查看习题详情和答案>>
①当该服装店获得14500元的利润时，售价为多少元？
②当售价定为多少元时，该服装店获得的利润最大？
某种商品的成本为5元/件，开始按8元/件销售，销售量为50件，为了获取最大利润，商家先后采取了提价与降价两种措施进行试销．经试销发现：销售价每上涨1元每天销售量就减少10件；而降价后，日销售量Q（件）与实际销售价x（元）满足关系Q=
（1）求总利润（利润=销售额-成本）y（元）与实际销售价x（件）的函数关系式；
（2）试问：当实际销售价为多少元时，总利润最大． 查看习题详情和答案>>
|
（1）求总利润（利润=销售额-成本）y（元）与实际销售价x（件）的函数关系式；
（2）试问：当实际销售价为多少元时，总利润最大． 查看习题详情和答案>>
（万元）与投入资金
（万元）成正比例关系，且当投入资金为6万元时，可获利润1.5
万元。生产R型产品所获利润
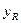（万元）与投入资金
（
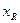万元）满足关系
,为获得最大总利润，问生产W、R型产品各应投入资金多少万元？获得的最大总利润是多少？