摘要:由圆锥曲线的范围引发的讨论 例11.我们把由半椭圆 与半椭圆 合成的曲线称作“果圆 .其中...如图.设点..是相应椭圆的焦点..和.是“果圆 与.轴的交点.是线段的中点. (1)若是边长为1的等边三角形.求该 “果圆 的方程, (2)设是“果圆 的半椭圆 上任意一点.求证:当取得最小值时. 在点或处, (3)若是“果圆 上任意一点.求取得最小值时点的横坐标. 分析: 本题中的果圆两部分之间的联系在于有共同的顶点.以此为据求解方程.则由距离公式转化为二次函数研究最值.但要注意圆锥曲线的范围.即得到二次函数的定义域.在其定义域内求函数的最值. 解:(1) . . 于是. 所求“果圆 方程为.. (2)设.则 . . 的最小值只能在或处取到. 即当取得最小值时.在点或处. (3).且和同时位于“果圆 的半椭圆和半椭圆上.所以.由(2)知.只需研究位于“果圆 的半椭圆上的情形即可. . 当.即时.的最小值在时取到. 此时的横坐标是. 当.即时.由于在时是递减的.的最小值在时取到.此时的横坐标是. 综上所述.若.当取得最小值时.点的横坐标是,若.当取得最小值时.点的横坐标是或. 评注:本题的创意在于把焦点在轴上和焦点在轴上的椭圆联为一体.看似陌生实质为基本知识.要善于发现解决问题的突破口.在把几何问题转化为函数问题时.应该有函数意识.寻求函数的定义域.即圆锥曲线的范围.并在定义域内求值域. 例12.已知椭圆C:=1的离心率为,短轴一个端点到右焦点的距离为. (Ⅰ)求椭圆C的方程; (Ⅱ)设直线l与椭圆C交于A.B两点.坐标原点O到直线l的距离为.求△AOB面积的最大值. 分析:要求三角形的面积.需要由斜截式写出直线的方程.解方程组求弦长和顶点到直线的距离.但用斜截式写方程时要注意其斜率是否存在.不定则需讨论. 解:(Ⅰ)设椭圆的半焦距为.依题意 .所求椭圆方程为. (Ⅱ)设.. (1)当轴时.. (2)当与轴不垂直时.设直线的方程为. 由已知.得. 把代入椭圆方程.整理得. .. . 当且仅当.即时等号成立.当时.. 综上所述. 当最大时.面积取最大值. 评注:在研究直线与圆锥曲线的位置关系时.要注意直线的斜率是否存在.一般要分情况讨论.
网址:http://m.1010jiajiao.com/timu_id_3980612[举报]
设点A,B的坐标分别为(-a,0),(a,0).直线AM,BM相交于点M,且他们的斜率之积为k.则下列说法正确的是
(1)当k=
时,点M的轨迹是双曲线.(其中a,b∈R+)
(2)当k=-
时,点M的轨迹是部分椭圆.(其中a,b∈R+)
(3)在(1)条件下,点p(x0,y0)(x0<0)是曲线上的点F1(-
,0),F2(
,0),且|PF1|=
|PF2|,则(1)的轨迹所在的圆锥曲线的离心率取值范围(1,
]
(4)在(2)的条件下,过点F1(-
,0),F2(
,0).满足
•
=0的点M总在曲线的内部,则(2)的轨迹所在的圆锥曲线的离心率的取值范围是(
,1).
查看习题详情和答案>>
(2)(3)
(2)(3)
(1)当k=
| b2 |
| a2 |
(2)当k=-
| b2 |
| a2 |
(3)在(1)条件下,点p(x0,y0)(x0<0)是曲线上的点F1(-
| a2+b2 |
| a2+b2 |
| 1 |
| 4 |
| 5 |
| 3 |
(4)在(2)的条件下,过点F1(-
| a2-b2 |
| a2-b2 |
. |
| MF1 |
. |
| MF2 |
| ||
| 2 |
 如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=
如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=| 17 |
(1)曲线段C是哪类圆锥曲线的一部分?并建立适当的坐标系,求曲线段C所在的圆锥曲线的标准方程;
(2)在(1)所建的坐标系下,已知点P(m,n)在曲线段C上,直线l:mx+ny=1,求直线l被圆x2+y2=1截得的弦长的取值范围.
与圆类似,连接圆锥曲线上两点的线段叫做圆锥曲线的弦.过有心曲线(椭圆、双曲线)中心(即对称中心)的弦叫做有心曲线的直径.对圆x2+y2=r2,由直径所对的圆周角是直角出发,可得:若AB是圆O的直径,M是圆O上异于A、B的一点,且AM,BM均与坐标轴不平行,则kAM•kBM=-1.类比到椭圆
+
=1,类似结论是
.
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
若AB是椭圆
+
=1的直径,M是椭圆上异于A、B的一点,且AM、BM均与坐标轴不平行,则kAM•kBM=-
.
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a2 |
若AB是椭圆
+
=1的直径,M是椭圆上异于A、B的一点,且AM、BM均与坐标轴不平行,则kAM•kBM=-
.
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a2 |
.
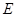 的两个焦点坐标是
的两个焦点坐标是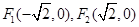 ,且离心率为
,且离心率为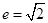 ;
;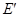 表示曲线
表示曲线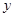 轴左边部分,若直线
轴左边部分,若直线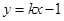 与曲线
与曲线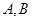 两点,求
两点,求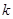 的取值范围;
的取值范围;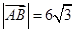 ,且曲线
,且曲线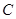 ,使
,使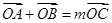 ,求
,求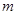 的值.
的值. 和
和 相交于点
相交于点 且
且 ,点
,点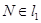 .以
.以 为端点的曲线段C上的任一点到
为端点的曲线段C上的任一点到 的距离相等.若
的距离相等.若 为锐角三角形,
为锐角三角形, ,
, ,且
,且 .
. 在曲线段C上,直线
在曲线段C上,直线 ,求直线
,求直线 被圆
被圆 截得的弦长的取值范围.
截得的弦长的取值范围.