摘要:[例1]如图.三棱锥D-ABC中.平面ABD.平面ABC均为等腰直角三角形.∠ABC=∠BAD=900.其腰BC=a.且二面角D-AB-C=600. (1) 求异面直线DA与BC所成的角, (2) 求异面直线BD与AC所成的角, (3) 求D到BC的距离, (4) 求异面直线BD与AC的距离. 解析:(1)DA与BC成600角 (2)设BE中点为O.DE中点为F.连OF.则OF//BD.求∠AOF即为 异面直线BD与AC成角在ΔAOF中可求得∠AOF =arccos (3)∵ BA⊥平面ADE ∴ 平面DAE⊥平面ABC故取AE中点M.则有DM⊥平面ABC,取BC中点N.由MN⊥BC.根据三垂线定理.DN⊥BC ∴ DN是D到BC的距离 在△DMN中.DM=a.MN=a ∴ DN=a (4)∵ BF平面BDF.AC平面BDF.AC∥BF ∴ AC∥平面BDF, 又BD平面BDF ∴ AC与BD的距离即AC到平面BDF的距离 ∵ . ∴ . 即异面直线BD与AC的距离为 ◆评注:三棱锥的等体积变换求高.也是求点到面距离的常用方法. [例2]如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AB⊥AD,AB∥DC,AB=4,AD=DC=2,侧面PAD是正三角形,且与底面垂直,M是PB的中点, (Ⅰ) 求证:CM∥侧面PAD, (Ⅱ)求直线CM与底面ABCD所成的角, (Ⅲ)求侧面PBC与侧面PAD所成二面角的大小 解:(Ⅰ)证明:作MN∥AB交AP于N,连结DN, 则MN∥AB∥CD,且 ∴CM∥ND,CM∥平面PAD (Ⅱ)∵CM∥ND, ∴ND与平面ABCD所成的角为所求. ∵侧面PAD⊥底面ABCD.∴ND在平面ABCD上的射影为AD ∴∠AND为所求, ∵⊿PAD是正三角形.N是PA的中点 ∴CM与底面所成的角为30º. (Ⅲ)延长AD.BC交于点E,连结P.E. 则PE为所求二面角的棱.且AD=DE=PD 所以.∠APE=90º.AP⊥PE 又∵AB⊥AD,平面PAD⊥底面ABCD ∴AB⊥平面PAE ∴BP⊥PE, ∠BPA为所求二面角的平面角 tan∠BPA= 所以.侧面PBC与侧面PAD所的角为arctan2 [例3]如图.已知二面角α-PQ-β为60°.点A和点B分别在平面α和平面 β 内.点C在棱PQ上.∠ACP=∠BCP=30°.CA=CB=a. (1)求证:AB⊥PQ, (2)求点B到平面α的距离, (3)设R是线段CA上的一点.直线BR与平面α所成的角为45°.求线段CR的长度. 证明(1):在平面β内作BD⊥PQ于D.连结AD. ∵∠ACP=∠BCP=30°.CA=CB=a.CD公用. ∴△ACD≌△BCD . ∴∠ADC=∠BDC= 90°.即AD⊥PQ.于是PQ⊥平面ABD. 则AB⊥PQ. 知.∠ADB是二面角α-PQ-β的平面角. ∴∠ADB=60°.又PQ⊥平面ABD. ∴α⊥平面ABD.过B作BE⊥AD于点E.则BE即为B到平面α的距离. BE=BD·sin60°=BC·sin30°·sin60°= a. (3) 解:连结ER.∵BE⊥α.∴∠BRE是BR与α所成的角. 即∠BRE=45°.则有BR== a.易知△ABD为正三角形.AB=AD=BD=a. 在△ABC中.由余弦定理得cos∠BCA=. 在△BCR中.设CR=x.由余弦定理得(a)2=x2+a2-2ax·.求得x1=.x2=(舍去.∵CR<AC=a).故CR=. [例4]四棱锥中.底面ABCD为平行四边形.侧面底面ABCD.已知,,,. (Ⅰ)证明:, (Ⅱ)求直线SD与平面SBC所成角的大小. 解:(1)作.垂足为.连结.由侧面底面.得底面. 因为.所以. 又.故为等腰直角三角形..由三垂线定理.得. 知.依题设. 故.由... 又.作.垂足为.则平面.连结.为直线与平面所成的角. ∴直线与平面SBC所成的角为.
网址:http://m.1010jiajiao.com/timu_id_3980395[举报]
 如图,以等腰直角三角形斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论:
如图,以等腰直角三角形斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论:①
| BD |
| AC |
②∠BAC=60°;
③三棱锥D-ABC是正三棱锥;
④平面ADC的法向量和平面ABC的法向量互相垂直.
其中正确的是( )
| A、①② | B、②③ | C、③④ | D、①④ |
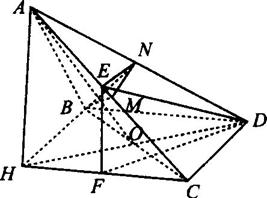
 如图所示,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜
如图所示,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=
| 3 |
(1)当正视图方向与向量
| CD |
(2)求二面角B-AC-D的余弦值;
(3)在线段AC上是否存在一点E,使ED与平面BCD成30°角?若存在,确定点E的位置;若不存在,说明理由.

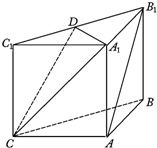 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,∠BAC=90°,点D是棱B1C1的中点.
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,∠BAC=90°,点D是棱B1C1的中点.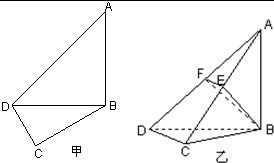 在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD沿BD折起,使平面ABD⊥平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.