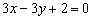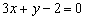摘要:(三)例题分析: 例1.(1).., (2).., (3)... 上述三个对应 是到的映射. 例2.已知集合.映射.在作用下点的象是.则集合 ( ) 解法要点:因为.所以. 例3.矩形的长.宽.动点.分别在.上.且.(1)将的面积表示为的函数.求函数的解析式, (2)求的最大值. 解:(1) . ∵.∴. ∴函数的解析式:, (2)∵在上单调递增.∴.即的最大值为. 例4.函数对一切实数.均有成立.且. (1)求的值, (2)对任意的..都有成立时.求的取值范围. 解:(1)由已知等式.令.得. 又∵.∴. (2)由.令得.由(1)知.∴. ∵.∴在上单调递增.∴. 要使任意.都有成立. 当时.,显然不成立. 当时..∴.解得 ∴的取值范围是.
网址:http://m.1010jiajiao.com/timu_id_3976446[举报]
(由理科第三册§3.8例2及文科第三册§2.5例2改编)如图,在边长为6cm的正方形铁皮的四角截去相等的正方形,将剩余部分沿虚线折起,做成无盖方底箱子,这个箱子的最大容积是( )

A.12 cm3 B.16 cm3 C.24cm3 D.36 cm3
查看习题详情和答案>>
几位同学对三元一次方程组
(其中系数ai,bi,ci(i=1,2,3)不全为零) 的解的情况进行研究后得到下列结论:
结论一:当D=0,且Dx=Dy=Dz=0时,方程组有无穷多解;
结论二:当D=0,且Dx,Dy,Dz都不为零时,方程组有无穷多解;
结论三:当D=0,且Dx=Dy=Dz=0时,方程组无解.
可惜的是这些结论都不正确.现在请你分析一下,下面给出的方程组可以作为结论一、二、三的反例分别是( )
(1)
; (2)
; (3)
.
|
结论一:当D=0,且Dx=Dy=Dz=0时,方程组有无穷多解;
结论二:当D=0,且Dx,Dy,Dz都不为零时,方程组有无穷多解;
结论三:当D=0,且Dx=Dy=Dz=0时,方程组无解.
可惜的是这些结论都不正确.现在请你分析一下,下面给出的方程组可以作为结论一、二、三的反例分别是( )
(1)
|
|
|
查看习题详情和答案>>
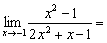 .
.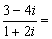 ( )
( )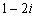 B.
B.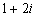 C.
C.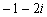 D.
D.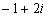
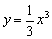 上的一点
上的一点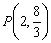 ,这条曲线的过点P的切线方程是( )
,这条曲线的过点P的切线方程是( )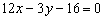 B.
B.