摘要：10．如图.已知A1B1C1-ABC是正三棱柱.D是AC中点． (1)证明AB1∥平面DBC1, (2)假设AB1⊥BC1.求以BC1为棱. DBC1与CBC1为面的二面角α的度数． (1)证明:∵A1B1C1-ABC是正三棱柱.∴四边形B1BCC1是矩形． 连结B1C交BC1于E.则B1E=EC．连结DE． 在△AB1C中.∵AD=DC.∴DE∥AB1． 又AB1平面DBC1.DE平面DBC1.∴AB1∥平面DBC1． (2)解:作DF⊥BC.垂足为F.则DF⊥面B1BCC1.连结EF.则EF 是ED在平面B1BCC1上的射影． ∵AB1⊥BC1. 由(1)知AB1∥DE.∴DE⊥BC1.则BC1⊥EF.∴∠DEF是二面角α的平面角． 设AC=1.则DC=．∵△ABC是正三角形. ∴在Rt△DCF中.DF=DC·sinC=. CF=DC·cosC=．取BC中点G． ∵EB=EC.∴EG⊥BC．在Rt△BEF中. EF2=BF·GF.又BF=BC-FC=.GF=. ∴EF2=·.即EF=． ∴tg∠DEF=． ∴∠DEF=45°故二面角α为45°． [探索题]
网址：http://m.1010jiajiao.com/timu_id_3975899[举报]
武汉臭豆腐闻名全国，某人买了两串臭豆腐，每串3颗（如图）．规定：每串臭豆腐只能至左向右一颗一颗地吃，且两串可以自由交替吃．请问：该人将这两串臭豆腐吃完，有20
20
种不同的吃法．（用数字作答）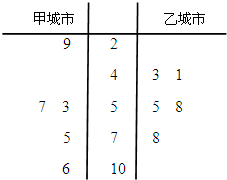
（2013•朝阳区一模）国家环境标准制定的空气质量指数与空气质量等级对应关系如下表：| 空气质量指数 | 0-50 | 51-100 | 101-150 | 151-200 | 201-300 | 300以上 |
| 空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
（Ⅰ）试根据上面的统计数据，判断甲、乙两个城市的空气质量指数的方差的大小关系（只需写出结果）；
（Ⅱ）试根据上面的统计数据，估计甲城市某一天空气质量等级为2级良的概率；
（Ⅲ）分别从甲城市和乙城市的统计数据中任取一个，试求这两个城市空气质量等级相同的概率．
（注：s2=
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
（2012•云南模拟）根据《中华人民共和国道路交通安全法》规定：车辆驾驶员血液酒精浓度在20-80mg/100ml（不含80）之间，属于酒后驾车；血液酒精浓度在80mg/100ml（含80）以上时，属醉酒驾车．据《法制晚报》报道，2010年3月15日至3 月28日，全国查处酒后驾车和醉酒驾车共28800人，如图是对这28800人酒后驾车血液中酒精含量进行检测所得结果的频率分布直方图，则属于醉酒驾车的人数约为4320
4320
．
如图是2007年在广州举行的全国少数民族运动会上，七位评委为某民族舞蹈演员打出的分数的茎叶统计图，（1）写出这七个数据；
（2）求若去掉一个最高分和一个最低分后所剩数据的平均数和方差．
国家教育部、体育总局和共青团中央曾共同号召，在全国各级各类学校要广泛、深入地开展全国亿万大中小学生阳光体育运动．为此某网站于2010年1月18日至24日，在全国范围内进行了持续一周的在线调查，随机抽取其中200名大中小学生的调查情况，就每天的睡眠时间分组整理如表所示：| 序号（i） | 每天睡眠时间 （小时） |
组中值 （mi） |
频数 | 频率 （fi） |
| 1 | [4，5） | 4.5 | 8 | 0.10 |
| 2 | [5，6） | 5.5 | 52 | 0.20 |
| 3 | [6，7） | 6.5 | 60 | 0.30 |
| 4 | [7，8） | 7.5 | 56 | 0.25 |
| 5 | [8，9） | 8.5 | 20 | 0.10 |
| 6 | [9，10） | 9.5 | 4 | 0.05 |
（2）该网站利用如图所示的算法流程图，对样本数据作进一步统计分析，求输出的S的值，并说明S的统计意义．