摘要:如图.三棱锥V-ABC中.VA⊥底面ABC. ∠ABC=90°. (1)求证:V.A.B.C四点在同一球面上, (2)过球心作一平面与底面内直线AB垂直.求证:此平面截三棱锥所得的截面是矩形. 证明:(1)取VC的中点M. ∵VA⊥底面ABC.∠ABC=90°. ∴BC⊥VB.在Rt△VBC中.M为斜边VC的中点. ∴MB=MC=MV.同理.在Rt△VAC中.MA=MV=MC. ∴MV=MC=MA=MB. ∴V.A.B.C四点在同一圆面上.M是球心. (2)取AC.AB.VB的中点分别为N.P.Q.连结NP.PQ.QM.MN.则MNPQ就是垂直于AB的三棱锥V-ABC的截面.易证PQMN是平行四边形.又VA⊥BC.QP∥VA.NP∥BC.∴QP⊥PN.故截面MNPQ是矩形.
网址:http://m.1010jiajiao.com/timu_id_3975898[举报]
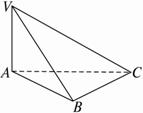
 15、如图,三棱锥V-ABC中,VA⊥底面ABC,∠ABC=90°.
15、如图,三棱锥V-ABC中,VA⊥底面ABC,∠ABC=90°.(1)求证:V、A、B、C四点在同一球面上;
(2)过球心作一平面与底面内直线AB垂直,求证:此平面截三棱锥所得的截面是矩形.
如图,三棱锥V—ABC中,VA⊥底面ABC,∠ABC=90°.
(1)求证:V、A、B、C四点在同一球面上;
(2)过球心作一平面与底面内直线AB垂直,求证:此平面截三棱锥所得的截面是矩形.
 ,则侧棱VA与底面所成角的大小为arcsin
,则侧棱VA与底面所成角的大小为arcsin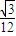 .(结果用反三角函数值表示)
.(结果用反三角函数值表示) ,则侧棱VA与底面所成角的大小为arcsin
,则侧棱VA与底面所成角的大小为arcsin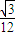 .(结果用反三角函数值表示)
.(结果用反三角函数值表示)