网址:http://m.1010jiajiao.com/timu_id_3974722[举报]
神舟七号宇宙飞船的航天员在准备出舱进行太空漫步时,意外发现舱门很难打开,有人臆测这可能与光压有关.已知光子的动能p、能量E与光速c的关系为E=pc,假设舱门的面积为1.0 m2,每平方公尺的舱门上每秒入射的光子能量为1.5 kJ,则舱门因反射光子而承受的力,最大约为多少牛顿?
( )
A.0.5×10-5 B.1.0×10-5
C.0.5×10-2 D.1.0×10-3
【解析】:平方公尺即为平方米.光子被舱门反射前后,光子动量变化量最大为Δp=2p(垂直入射与反射时),又因为E=pc,即对应于光子入射的能量为E时光子的动量改变量为Δp=,取Δt时间内入射的所有光子作为研究对象,由题意知Δt内与舱门发生作用的光子总能量为E总=Δt×1.5 kJ,根据动量定理FΔt=Δp总有F===,则:F=N=1.0×10-5N,B正确.
查看习题详情和答案>>
神舟七号宇宙飞船的航天员在准备出舱进行太空漫步时,意外发现舱门很难打开,有人臆测这可能与光压有关.已知光子的动能p、能量E与光速c的关系为E=pc,假设舱门的面积为1.0 m2,每平方公尺的舱门上每秒入射的光子能量为1.5 kJ,则舱门因反射光子而承受的力,最大约为多少牛顿?
( )
A.0.5×10-5 B.1.0×10-5
C.0.5×10-2 D.1.0×10-3
【解析】:平方公尺即为平方米.光子被舱门反射前后,光子动量变化量最大为Δp=2p(垂直入射与反射时),又因为E=pc,即对应于光子入射的能量为E时光子的动量改变量为Δp=,取Δt时间内入射的所有光子作为研究对象,由题意知Δt内与舱门发生作用的光子总能量为E总=Δt×1.5 kJ,根据动量定理FΔt=Δp总有F===,则:F=N=1.0×10-5N,B正确.
查看习题详情和答案>>
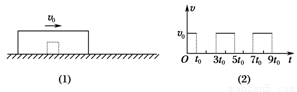
一个物体静置于光滑水平面上,外面扣一质量为M的盒子,如图(1)所示.现给盒子一初速度v0,此后,盒子运动的v-t图象呈周期性变化,如图(2)所示.请据此求盒内物体的质量.
【解析】:设物体的质量为m,t0时刻受盒子碰撞获得速度v,根据动量守恒定律
Mv0=mv,①
3t0时刻物体与盒子右壁碰撞使盒子速度又变为v0,说明碰撞是弹性碰撞
mv=mv2,②
联立①②解得m=M.
(也可通过图象分析得出v0=v,结合动量守恒,得出正确结果)
查看习题详情和答案>>