摘要:17. (Ⅰ)解:∵函数的图象过点. ∴. ∴. ① 又函数图象在点处的切线斜率为8. ∴ . 又. ∴. ② 解由①②组成的方程组.可得. 得. 令.可得, 令.可得. ∴函数的单调增区间为.减区间为.
网址:http://m.1010jiajiao.com/timu_id_3972939[举报]
(本小题满分14分)已知函数![]() 满足:
满足:![]() ;(1)分别写出
;(1)分别写出![]() 时
时![]() 的解析式
的解析式![]() 和
和![]() 时
时![]() 的解析式
的解析式![]() ;并猜想
;并猜想![]() 时
时![]() 的解析式
的解析式![]() (用
(用![]() 和
和![]() 表示)(不必证明)(2分)(2)当
表示)(不必证明)(2分)(2)当![]()
![]() 时,
时,![]()
![]() 的图象上有点列
的图象上有点列![]() 和点列
和点列![]() ,线段
,线段![]() 与线段
与线段![]() 的交点
的交点![]() ,求点
,求点![]() 的坐标
的坐标![]() ;(4分)
;(4分)
(3)在前面(1)(2)的基础上,请你提出一个点列![]() 的问题,并进行研究,并写下你研究的过程 (8分)
的问题,并进行研究,并写下你研究的过程 (8分)
(本小题满分14分)已知函数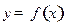 满足:
满足: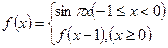 ;(1)分别写出
;(1)分别写出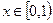 时
时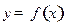 的解析式
的解析式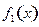 和
和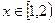 时
时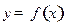 的解析式
的解析式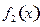 ;并猜想
;并猜想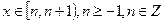 时
时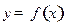 的解析式
的解析式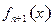 (用
(用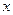 和
和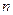 表示)(不必证明)(2分)(2)当
表示)(不必证明)(2分)(2)当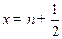
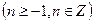 时,
时,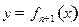
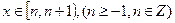 的图象上有点列
的图象上有点列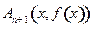 和点列
和点列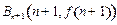 ,线段
,线段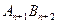 与线段
与线段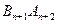 的交点
的交点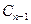 ,求点
,求点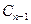 的坐标
的坐标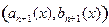 ;(4分)
;(4分)
(3)在前面(1)(2)的基础上,请你提出一个点列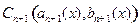 的问题,并进行研究,并写下你研究的过程 (8分)
的问题,并进行研究,并写下你研究的过程 (8分)
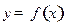 满足:
满足: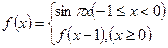 ;(1)分别写出
;(1)分别写出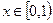 时
时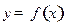 的解析式
的解析式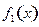 和
和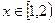 时
时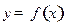 的解析式
的解析式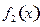 ;并猜想
;并猜想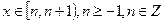 时
时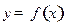 的解析式
的解析式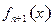 (用
(用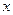 和
和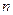 表示)(不必证明)(2分)(2)当
表示)(不必证明)(2分)(2)当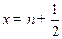
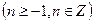 时,
时,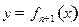
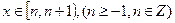 的图象上有点列
的图象上有点列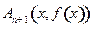 和点列
和点列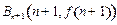 ,线段
,线段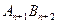 与线段
与线段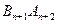 的交点
的交点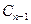 ,求点
,求点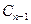 的坐标
的坐标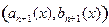 ;(4分)
;(4分)(3)在前面(1)(2)的基础上,请你提出一个点列
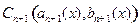 的问题,并进行研究,并写下你研究的过程 (8分)
的问题,并进行研究,并写下你研究的过程 (8分)(本小题满分14分)已知二次函数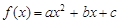 满足:①
满足:①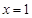 时有极值;②图象过点
时有极值;②图象过点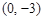 ,且在该点处的切线斜率为
,且在该点处的切线斜率为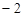 .
.
(I) 求f(x)的解析式;
(II)若曲线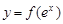 上任意一点的切线的斜率恒大于
上任意一点的切线的斜率恒大于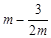 ,求
,求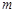 的取值范围;
的取值范围;
(Ⅲ)当非零实数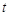 满足什么条件时,函数
满足什么条件时,函数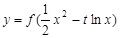 的图象与坐标轴没有公共点?
的图象与坐标轴没有公共点?
查看习题详情和答案>>