摘要：10．在极坐标系中.圆C的圆心C(6.).半径r＝6. (1)写出圆C的极坐标方程, (2)若Q点在圆C上运动.P在OQ的延长线上.且OQ∶QP＝3∶2.求动点P的轨迹方程． 解:(1)圆C的极坐标方程ρ＝12cos(θ-), (2)设P的坐标为(ρ.θ).因为P在OQ的延长线上. 即OQ∶QP＝3∶2.所以点Q的坐标为(ρ.θ). 若Q点在圆C上运动. 则ρ＝12cos(θ-). 即ρ＝20cos(θ-). 故点P的轨迹方程为ρ＝20cos(θ-)．
网址：http://m.1010jiajiao.com/timu_id_3971646[举报]
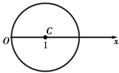如图，在极坐标系中，圆C的圆心坐标为（1，0），半径为1．（Ⅰ）求圆C的极坐标方程；
（Ⅱ）若以极点O为原点，极轴所在直线为x轴建立平面直角坐标系．已知直线l的参数方程为
|
在极坐标系中，已知圆C的圆心C(3，
)，半径r=1，Q点在圆C上运动．
（1）求圆C的极坐标方程；
（2）若P在直线OQ上运动，且
=
，求动点P轨迹的极坐标方程．
查看习题详情和答案>>
| π |
| 6 |
（1）求圆C的极坐标方程；
（2）若P在直线OQ上运动，且
. |
| OQ |
| 2 |
| 3 |
. |
| QP |