摘要:已知△ABC的角A.B.C所对的边分别是a.b.c.设向量m=(a.b).n=(sinB.sinA).p=(b-2.a-2). (1)若m∥n.求证:△ABC为等腰三角形, (2)若m⊥p.边长c=2.角C=.求△ABC的面积. 解:(1)证明:∵m∥n.∴asinA=bsinB. 即a·=b·. 其中R是△ABC外接圆半径.∴a=b. ∴△ABC为等腰三角形. (2)由题意可知m·p=0.即a(b-2)+b(a-2)=0. ∴a+b=ab. 由余弦定理可知.4=a2+b2-ab=(a+b)2-3ab. 即(ab)2-3ab-4=0. ∴ab=4(舍去ab=-1). ∴S=absinC=×4×sin=.
网址:http://m.1010jiajiao.com/timu_id_3971601[举报]
已知△ABC的角A、B、C所对的边分别是a、b、c,设向量
=(a,b),
=(sinB,sinA),
=(b-2,a-2).
(1)若
∥
,求证:△ABC为等腰三角形;
(2)若
⊥
,边长c=2,角C=
,求△ABC的面积.
查看习题详情和答案>>
| m |
| n |
| p |
(1)若
| m |
| n |
(2)若
| m |
| p |
| π |
| 3 |
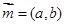 ,
,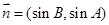 ,
,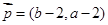 .
. //
// ,求证:ΔABC为等腰三角形;
,求证:ΔABC为等腰三角形; 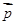 ,边长c = 2,角C =
,边长c = 2,角C = 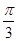 ,求ΔABC的面积 .
,求ΔABC的面积 .