摘要：定义:在数列{an}中.an＞0且an≠1.若为定值.则称数列{an}为“等幂数列 .已知数列{an}为“等幂数列 .且a1＝2.a2＝4.Sn为数列{an}的前n项和.则S2009＝ ( ) A.6026 B .6024 C.2 D.4 解析:＝24＝16＝＝4a3. 得a3＝2.同理得a4＝4.a5＝2.-. 这是一个周期数列. ∴S2009＝×(2+4)+2＝6026. 答案:A
网址：http://m.1010jiajiao.com/timu_id_3971485[举报]
定义：在数列{an}中，an＞0且an≠1，若
为定值，则称数列{an}为“等幂数列”．已知数列{an}为“等幂数列”，且a1=2，a2=4，Sn为数列{an}的前n项和，则S2009=（ ）
| a | an+1 n |
| A、6026 | B、6024 |
| C、2 | D、4 |
定义：在数列{an}中，an＞0且an≠1，若anan+1为定值，则称数列{an}为“等幂数列”．已知数列{an}为“等幂数列”，且a1=2，a2=4，Sn为数列{an}的前n项和，则S2013等于（ ）
查看习题详情和答案>>
.定义：在数列{an}中，an＞0且an≠1，若
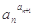为定值，则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”，且a1＝2，a2＝4，Sn为数列{an}的前n项和，则S2009＝ （ ）A.6026
B .6024 C.2
D.4
查看习题详情和答案>>
为定值，则称数列{an}为“等幂数列”．已知数列{an}为“等幂数列”，且a1=2，a2=4，Sn为数列{an}的前n项和，则S2009=（ ）
为定值，则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”，且a1＝2，a2＝4，Sn为数列{an}的前n项和，则S2009＝ （ ）