摘要:定义在R上的函数f(x)满足f(x)=f(x+4).当2≤x≤6时.f(x)= ()||+n.f(4)=31. (1)求m.n的值, (2)比较f(log3m)与f(log3n)的大小. 解:(1)因为函数f(x)在R上满足f(x)=f(x+4). 所以4是函数f(x)的一个周期. 可得f(2)=f+n=()+n. ① 又f+n=31. ② 联立①②组成方程组解得m=4.n=30. 知.函数f(x)=()+30.x∈[2,6]. 因为1<log34<2.所以5<log34+4<6. f(log3m)=f(log34)=f(log34+4) =()+30 =()|log34|+30. 又因为3<log330<4.
网址:http://m.1010jiajiao.com/timu_id_3971478[举报]
定义在R上的函数f(x)满足f(x)=f(x+2),当x∈[3,5]时,f(x)=2-|x-4|,则( )
(A)f(sin )<f(cos
)<f(cos ) (B)f(sin1)>f(cos1)
) (B)f(sin1)>f(cos1)
(C)f(cos )<f(sin
)<f(sin ) (D)f(cos2)>f(sin2)
) (D)f(cos2)>f(sin2)
查看习题详情和答案>>
定义在R上的函数f(x)满足f(x)=f(x+2),当x∈[3,5]时,f(x)=2-|x-4|,则( )
A.f(sin )<f(cos )<f(cos ) ) | B.f(sin1)>f(cos1) |
C.f(cos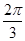 )<f(sin )<f(sin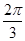 ) ) | D.f(cos2)>f(sin2) |
 )<f(cos
)<f(cos )<f(sin
)<f(sin