摘要:某公司生产一种产品的固定成本为0.5万元.但每生产100件需再增加 成本0.25万元.市场对此产品的年需求量为500件.年销售收入为R(t)=5t-(0≤t≤5).其中t为产品售出的数量. (1)把年利润表示为年产量x(x≥0)的函数f(x), (2)当年产量为多少件时.公司可获得最大年利润? 解:(1)当0≤x≤5时.f(x)=R(x)-0.5-0.25x =-x2+4.75x-0.5,当x>5时. f(x)=R(5)-0.5-0.25x=12-0.25x. 故所求函数解析式为 (2)0≤x≤5时.f(x)=-(x-4.75)2+10.78125. ∴在x=4.75时. f(x)有最大值10.78125.当x>5时. f(x)=12-0.25x<12-0.25×5 =10.75<10.78125. 综上所述.当x=4.75时.f(x)有最大值.即当年产量为475件时.公司可获得最大年利润.
网址:http://m.1010jiajiao.com/timu_id_3971477[举报]
某公司生产一种产品的固定成本为0.5万元,但每生产100件需再增加成本0.25万元,市场对此产品的年需求量为500件,年销售收入(单位:万元)为R(t)=5t-
(0≤t≤5),其中t为产品售出的数量(单位:百件).
(1)把年利润表示为年产量x(百件)(x≥0)的函数f(x);
(2)当年产量为多少件时,公司可获得最大年利润? 查看习题详情和答案>>
| t2 | 2 |
(1)把年利润表示为年产量x(百件)(x≥0)的函数f(x);
(2)当年产量为多少件时,公司可获得最大年利润? 查看习题详情和答案>>
某公司生产一种产品的固定成本为0.5万元,但每生产100件需再增加成本0.25万元,市场对此产品的年需求量为500件,年销售收入(单位:万元)为R(t)=5t- (0≤t≤5),其中t为产品售出的数量(单位:百件).
(0≤t≤5),其中t为产品售出的数量(单位:百件).
(1)把年利润表示为年产量x(百件)(x≥0)的函数f(x);
(2)当年产量为多少件时,公司可获得最大年利润?
查看习题详情和答案>>
某公司生产一种产品的固定成本为0.5万元,但每生产100件需再增加成本0.25万元,市场对此产品的年需求量为500件,年销售收入(单位:万元)为R(t)=5t-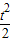 (0≤t≤5),其中t为产品售出的数量(单位:百件).
(0≤t≤5),其中t为产品售出的数量(单位:百件).
(1)把年利润表示为年产量x(百件)(x≥0)的函数f(x);
(2)当年产量为多少件时,公司可获得最大年利润?
查看习题详情和答案>>
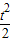 (0≤t≤5),其中t为产品售出的数量(单位:百件).
(0≤t≤5),其中t为产品售出的数量(单位:百件).(1)把年利润表示为年产量x(百件)(x≥0)的函数f(x);
(2)当年产量为多少件时,公司可获得最大年利润?
查看习题详情和答案>>
 (0≤t≤5),其中t为产品售出的数量(单位:百件).
(0≤t≤5),其中t为产品售出的数量(单位:百件).