摘要：17．若a1＞0.a1≠1.an+1＝(n＝1,2.-) (1)求证:an+1≠an, (2)令a1＝.写出a2.a3.a4.a5的值.观察并归纳出这个数列的通项公式an. 解:．若an+1＝an. 即＝an.解得an＝0,1. 从而an＝an-1＝-＝a2＝a1＝0,1.与题设a1＞0.a1≠1相矛盾. 故an+1≠an成立． (2)a1＝.a2＝.a3＝.a4＝.a5＝.an＝. n∈N*.
网址：http://m.1010jiajiao.com/timu_id_3971307[举报]
(本小题12分) 正项数列{an}满足a1=2，点An（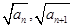
）在双曲线y2-x2=1上，点（
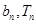）在直线y=-
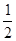x+1上，其中Tn是数列{bn}的前n项和。
①求数列{an}、{bn}的通项公式；
②设Cn=anbn，证明 Cn+1＜Cn
③若m-7anbn＞0恒成立，求正整数m的最小值。
查看习题详情和答案>>
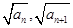）在双曲线y2-x2=1上，点（
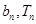）在直线y=-
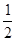x+1上，其中Tn是数列{bn}的前n项和。
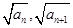）在双曲线y2-x2=1上，点（
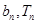）在直线y=-
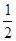x+1上，其中Tn是数列{bn}的前n项和。