摘要：19．已知圆(x-2)2+(y-1)2＝.椭圆b2x2+a2y2＝a2b2(a>b>0)的离心率为.若圆与椭圆相交于A.B.且线段AB是圆的直径.求椭圆的方程． 解:∵e＝＝＝.∴a2＝2b2. 因此.所求椭圆的方程为x2+2y2＝2b2. 又∵AB为直径.是线段AB的中点. 设A(2-m,1-n).B(2+m,1+n).则 ⇒ ⇒得2b2＝16. 故所求椭圆的方程为x2+2y2＝16.
网址：http://m.1010jiajiao.com/timu_id_3971288[举报]
(本小题满分12分)
已知圆C1的方程为(x－2)2+(y－1)2=
，椭圆C2的方程为
，C2的离心率为
，如果C1与C2相交于A、B两点，且线段AB恰为圆C1的直径，试求：
（1）直线AB的方程；（2）椭圆C2的方程.
(本小题满分12分)
已知圆C1的方程为(x－2)2+(y－1)2=
，椭圆C2的方程为
，C2的离心率为
，如果C1与C2相交于A、B两点，且线段AB恰为圆C1的直径，试求：
（1）直线AB的方程；（2）椭圆C2的方程.
查看习题详情和答案>>
(本小题满分12分)
已知圆C1的方程为(x－2)2+(y－1)2=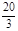
，椭圆C2的方程为
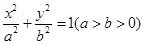，C2的离心率为
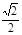，如果C1与C2相交于A、B两点，且线段AB恰为圆C1的直径，试求：
（1）直线AB的方程；（2）椭圆C2的方程.
已知圆C1的方程为(x－2)2+(y－1)2=
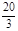，椭圆C2的方程为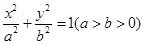，C2的离心率为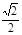，如果C1与C2相交于A、B两点，且线段AB恰为圆C1的直径，试求：（1）直线AB的方程；（2）椭圆C2的方程.
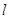,使得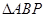
的面积最大时点P的坐标.
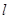,使得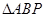
的面积最大时点P的坐标.