摘要:已知数列{an}满足:a1=.a2=.an+1=2an-an-1(n≥2.n∈N*).数列{bn}满足b1<0,3bn-bn-1=n(n≥2.n∈N*).数列{bn}的前n项和为Sn. (1)求数列{an}的通项an, (2)求证:数列{bn-an}为等比数列. 解:(1)证明∵2an=an+1+an-1(n≥2.n∈N*). ∴{an}是等差数列. 又∵a1=.a2=.∴an=+(n-1)·=. (2)证明:∵bn=bn-1+(n≥2.n∈N*). ∴bn+1-an+1=bn+-=bn- =(bn-)=(bn-an). 又∵b1-a1=b1-≠0. ∴{bn-an}是以b1-为首项.以为公比的等比数列.
网址:http://m.1010jiajiao.com/timu_id_3971265[举报]
(本小题满分12分)已知数列{an}的前n项和为Sn, 且满足条件:4S n =![]() + 4n – 1 , nÎN*.
+ 4n – 1 , nÎN*.
(1) 证明:(a n– 2)2 –![]() =0 (n ³ 2);(2) 满足条件的数列不惟一,试至少求出数列{an}的的3个不同的通项公式 .
=0 (n ³ 2);(2) 满足条件的数列不惟一,试至少求出数列{an}的的3个不同的通项公式 .
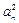 + 4n – 1 , nÎN*.
+ 4n – 1 , nÎN*.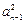 ="0" (n ³ 2);(2) 满足条件的数列不惟一,试至少求出数列{an}的的3个不同的通项公式 .
="0" (n ³ 2);(2) 满足条件的数列不惟一,试至少求出数列{an}的的3个不同的通项公式 .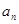 }满足:
}满足: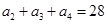 ,且
,且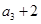 是
是 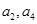 的等差中
的等差中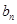 =
=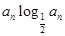 ,sn为数列
,sn为数列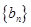 的前
的前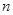 项和,求证:sn
项和,求证:sn 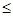
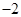 .
.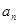 }满足:
}满足: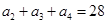 ,且
,且 是
是 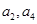 的等差中
的等差中 =
=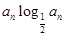 ,sn为数列
,sn为数列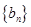 的前
的前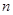 项和,求证:sn
项和,求证:sn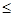
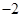 .
. ,记数列{bn}的前n项和为Tn,
,记数列{bn}的前n项和为Tn, (n∈N*).
(n∈N*).