摘要:骤)16.如图所示是一个几何体的直观图.正视图.俯视图.侧视图(其中正视图为直角梯形.俯视图为正方形.侧视图为直角三角形.尺寸如图所示). (1)求四棱锥P-ABCD的体积, (2)证明:BD∥平面PEC, (3)若G为BC上的动点.求证:AE⊥PG. 解:(1)由几何体的三视图可知.底面ABCD是边长为4的正方形.PA⊥平面ABCD.PA∥EB.且PA=4.BE=2.AB=AD=CD=CB=4. ∴VP-ABCD=PA×SABCD=×4×4×4=. (2)证明:连结AC交BD于O点. 取PC中点F.连结OF. ∵EB∥PA.且EB=PA. 又OF∥PA.且OF=PA. ∴EB∥OF.且EB=OF. ∴四边形EBOF为平行四边形. ∴EF∥BD. 又EF⊂平面PEC.BD⊄平面PEC.所以BD∥平面PEC. (3)连结BP.∵==.∠EBA=∠BAP=90°. ∴△EBA∽△BAP.∴∠PBA=∠BEA. ∴∠PBA+∠BAE=∠BEA+∠BAE=90°. ∴PB⊥AE. 又∵BC⊥平面APEB.∴BC⊥AE. ∴AE⊥平面PBG.∴AE⊥PG.
网址:http://m.1010jiajiao.com/timu_id_3971180[举报]
解答题(本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤。)
16.(本小题满分为12分)
已知函数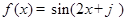 和
和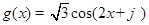 .
.
(Ⅰ)设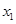 是
是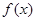 的极大值点,
的极大值点,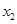 是
是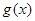 的极小值点,求
的极小值点,求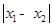 的最小值;
的最小值;
(Ⅱ)若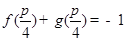 ,且
,且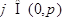 ,求
,求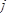 的值.
的值.
查看习题详情和答案>>
解答题(本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤。)
16.(本小题满分为12分)
已知函数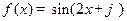 和
和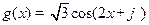 .
.
(Ⅰ)设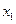 是
是 的极大值点,
的极大值点, 是
是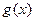 的极小值点,求
的极小值点,求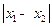 的最小值;
的最小值;
(Ⅱ)若 ,且
,且 ,求
,求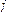 的值.
的值.
 ,定义函数
,定义函数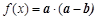
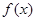 最小正周期;
最小正周期; ,求边AC的长.
,求边AC的长.