摘要:1.n 个数据..--.的平均数或平均值一般记为=.
网址:http://m.1010jiajiao.com/timu_id_3970759[举报]
平面直角坐标系xOy中,已知A1(x1,y1),A2(x2,y2),…,An(xn,yn)是直线l:y=kx+b上的n个点
(n∈N*,k、b均为非零常数).
(1)若数列{xn}成等差数列,求证:数列{yn}也成等差数列;
(2)若点P是直线l上一点,且
=a1
+a2
,求a1+a2的值;
(3)若点P满足
=a1
+a2
+…+an
,我们称
是向量
,
,…,
的线性组合,{an}是该线性组合的系数数列.当
是向量
,
,…,
的线性组合时,请参考以下线索:
①系数数列{an}需满足怎样的条件,点P会落在直线l上?
②若点P落在直线l上,系数数列{an}会满足怎样的结论?
③能否根据你给出的系数数列{an}满足的条件,确定在直线l上的点P的个数或坐标?
试提出一个相关命题(或猜想)并开展研究,写出你的研究过程.[本小题将根据你提出的命题(或猜想)的完备程度和研究过程中体现的思维层次,给予不同的评分]. 查看习题详情和答案>>
(n∈N*,k、b均为非零常数).
(1)若数列{xn}成等差数列,求证:数列{yn}也成等差数列;
(2)若点P是直线l上一点,且
| OP |
| OA1 |
| OA2 |
(3)若点P满足
| OP |
| OA1 |
| OA2 |
| OAn |
| OP |
| OA1 |
| OA2 |
| OAn |
| OP |
| OA1 |
| OA2 |
| OAn |
①系数数列{an}需满足怎样的条件,点P会落在直线l上?
②若点P落在直线l上,系数数列{an}会满足怎样的结论?
③能否根据你给出的系数数列{an}满足的条件,确定在直线l上的点P的个数或坐标?
试提出一个相关命题(或猜想)并开展研究,写出你的研究过程.[本小题将根据你提出的命题(或猜想)的完备程度和研究过程中体现的思维层次,给予不同的评分]. 查看习题详情和答案>>
平面直角坐标系xOy中,已知A1(x1,y1),A2(x2,y2),…,An(xn,yn)是直线l:y=kx+b上的n个点
(n∈N*,k、b均为非零常数).
(1)若数列{xn}成等差数列,求证:数列{yn}也成等差数列;
(2)若点P是直线l上一点,且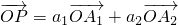 ,求a1+a2的值;
,求a1+a2的值;
(3)若点P满足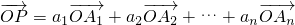 ,我们称
,我们称 是向量
是向量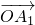 ,
, ,…,
,…,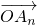 的线性组合,{an}是该线性组合的系数数列.当
的线性组合,{an}是该线性组合的系数数列.当 是向量
是向量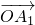 ,
, ,…,
,…,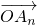 的线性组合时,请参考以下线索:
的线性组合时,请参考以下线索:
①系数数列{an}需满足怎样的条件,点P会落在直线l上?
②若点P落在直线l上,系数数列{an}会满足怎样的结论?
③能否根据你给出的系数数列{an}满足的条件,确定在直线l上的点P的个数或坐标?
试提出一个相关命题(或猜想)并开展研究,写出你的研究过程.[本小题将根据你提出的命题(或猜想)的完备程度和研究过程中体现的思维层次,给予不同的评分].
查看习题详情和答案>>
平面直角坐标系xOy中,已知A1(x1,y1),A2(x2,y2),…,An(xn,yn)是直线l:y=kx+b上的n个点
(n∈N*,k、b均为非零常数).
(1)若数列{xn}成等差数列,求证:数列{yn}也成等差数列;
(2)若点P是直线l上一点,且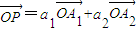 ,求a1+a2的值;
,求a1+a2的值;
(3)若点P满足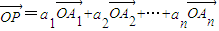 ,我们称
,我们称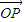 是向量
是向量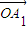 ,
,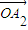 ,…,
,…,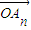 的线性组合,{an}是该线性组合的系数数列.当
的线性组合,{an}是该线性组合的系数数列.当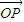 是向量
是向量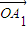 ,
,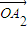 ,…,
,…,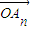 的线性组合时,请参考以下线索:
的线性组合时,请参考以下线索:
①系数数列{an}需满足怎样的条件,点P会落在直线l上?
②若点P落在直线l上,系数数列{an}会满足怎样的结论?
③能否根据你给出的系数数列{an}满足的条件,确定在直线l上的点P的个数或坐标?
试提出一个相关命题(或猜想)并开展研究,写出你的研究过程.[本小题将根据你提出的命题(或猜想)的完备程度和研究过程中体现的思维层次,给予不同的评分].
查看习题详情和答案>>
(n∈N*,k、b均为非零常数).
(1)若数列{xn}成等差数列,求证:数列{yn}也成等差数列;
(2)若点P是直线l上一点,且
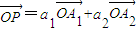 ,求a1+a2的值;
,求a1+a2的值;(3)若点P满足
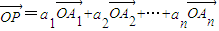 ,我们称
,我们称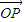 是向量
是向量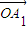 ,
,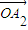 ,…,
,…,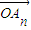 的线性组合,{an}是该线性组合的系数数列.当
的线性组合,{an}是该线性组合的系数数列.当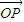 是向量
是向量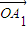 ,
,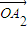 ,…,
,…,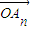 的线性组合时,请参考以下线索:
的线性组合时,请参考以下线索:①系数数列{an}需满足怎样的条件,点P会落在直线l上?
②若点P落在直线l上,系数数列{an}会满足怎样的结论?
③能否根据你给出的系数数列{an}满足的条件,确定在直线l上的点P的个数或坐标?
试提出一个相关命题(或猜想)并开展研究,写出你的研究过程.[本小题将根据你提出的命题(或猜想)的完备程度和研究过程中体现的思维层次,给予不同的评分].
查看习题详情和答案>>
在标准正态分布中我们常设P(X<x0)=Φ(x0),根据标准正态曲线的对称性有性质:P(X>x0)=1-Φ(x0).若X~N(μ,σ2),记P(X<x0)=F(x0)=Φ( ).
).
某市有280名高一学生参加计算机操作比赛,等级分为10分,随机调阅了60名学生的成绩,见下表:
成绩(分) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
人数(个) | 0 | 0 | 0 | 6 | 15 | 21 | 12 | 3 | 3 | 0 |
(1)求样本的平均成绩和标准差;
(2)若总体服从正态分布,求正态曲线的近似方程(提示:μ,σ分别可用样本的均值和标准差估计);
(3)若规定比赛成绩在7分或7分以上的学生参加省级比赛,试估计有多少学生可以进入省级比赛?(参考数值:φ(0.82)=0.793 9)