摘要:(二)圆锥曲线方程 1.掌握椭圆的定义.标准方程和椭圆的简单几何性质. 2.掌握双曲线的定义.标准方程和双曲线的简单几何性质. 3.掌握抛物线的定义.标准方程和抛物线的简单几何性质. 4.了解圆锥曲线的初步应用.
网址:http://m.1010jiajiao.com/timu_id_3970669[举报]
 (2013•浦东新区二模)(1)设椭圆C1:
(2013•浦东新区二模)(1)设椭圆C1:| x2 |
| a2 |
| y2 |
| b2 |
| 9y2 |
| 8 |
我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”.
(2)如图,已知“盾圆D”的方程为y2=
|
(3)由抛物线弧E1:y2=4x(0≤x≤
| 2 |
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
| r1 |
| r2 |
(2009•奉贤区二模)已知:点P与点F(2,0)的距离比它到直线x+4=0的距离小2,若记点P的轨迹为曲线C.
(1)求曲线C的方程.
(2)若直线L与曲线C相交于A、B两点,且OA⊥OB.求证:直线L过定点,并求出该定点的坐标.
(3)试利用所学圆锥曲线知识参照(2)设计一个与直线L过定点有关的数学问题,并解答所提问题.
查看习题详情和答案>>
(1)求曲线C的方程.
(2)若直线L与曲线C相交于A、B两点,且OA⊥OB.求证:直线L过定点,并求出该定点的坐标.
(3)试利用所学圆锥曲线知识参照(2)设计一个与直线L过定点有关的数学问题,并解答所提问题.
以下各个关于圆锥曲线的命题中
①设定点F1(0,-3),F2(0,3),动点P(x,y)满足条件|PF1|+|PF2|=a(a>0),则动点P的轨迹是椭圆或线段;
②过点(0,1)作直线,使它与抛物线y2=4x仅有一个公共点,这样的直线有3条;
③离心率为
,长轴长为8的椭圆标准方程为
+
=1;
④若3<k<4,则二次曲线
+
=1的焦点坐标是(±1,0).
其中真命题的序号为
查看习题详情和答案>>
①设定点F1(0,-3),F2(0,3),动点P(x,y)满足条件|PF1|+|PF2|=a(a>0),则动点P的轨迹是椭圆或线段;
②过点(0,1)作直线,使它与抛物线y2=4x仅有一个公共点,这样的直线有3条;
③离心率为
| 1 |
| 2 |
| x2 |
| 16 |
| y2 |
| 12 |
④若3<k<4,则二次曲线
| x2 |
| 4-k |
| y2 |
| 3-k |
其中真命题的序号为
②④
②④
(写出所有真命题的序号) ,长轴长为8的椭圆标准方程为
,长轴长为8的椭圆标准方程为 ;
; 的焦点坐标是(±1,0).
的焦点坐标是(±1,0). ,长轴长为8的椭圆标准方程为
,长轴长为8的椭圆标准方程为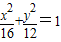 ;
;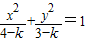 的焦点坐标是(±1,0).
的焦点坐标是(±1,0).