网址:http://m.1010jiajiao.com/timu_id_3966606[举报]
消费金额(元)的范围 | [200,400) | [400,500) | [500,700) | [700,900) | … |
获得奖券的金额(元) | 30 | 60 | 100 | 130 | … |
根据上述促销方法,顾客在该商场购物可以获得双重优惠.例如,购买标价为400元的商品,则消费金额为320元,获得的优惠额为400×0.2+30=110(元).设购买商品得到的优惠率=![]() .试问:
.试问:
(1)若购买一件标价为1 000元的商品,顾客得到的优惠率是多少?
(2)对于标价在[500,800](元)内的商品,顾客购买标价为多少元的商品,可得到不小于![]() 的优惠率?
的优惠率?
消费金额 (元)的范围 | [200,400) | [400,500) | [500,700) | [700,900] | … |
获得奖券 的金额(元) | 30 | 60 | 100 | 130 | … |
根据上述促销方法,顾客在该商场购物可以获得双重优惠,例如,购买标价为400元的商品,则消费金额为320元,获得的优惠额为:400×0.2+30=110元.
设购买商品得到的优惠率=![]() ,试问:
,试问:
(1)若购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)对于标价在[500,800](元)内的商品,顾客购买标价为多少元的商品,可得到不少于![]() 的优惠率?
的优惠率?
某商场在促销期间规定:商场内所有商品按标价的80%出售;同时,当顾客在该商场内消费满一定金额后,按如下方案获得相应金额的奖券:
|
消费金额(元)的范围 |
[200,400] |
[400,500) |
[500,700] |
[700,900] |
… |
|
获得奖券的金额(元) |
30 |
60 |
100 |
130 |
… |
根据上述促销方法,顾客在该商场购物可以获得双重优惠.例如,购买标价为400元的商品,则消费金额为320元,获得的优惠额为:400×0.2+30=110(元).设购买商品得到的优惠率=![]() .试问:
.试问:
(1)若购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)对于标价在[500,800](元)内的商品,顾客购买标价为多少元的商品,可得到不小于![]() 的优惠率?
的优惠率?
查看习题详情和答案>>
|
消费金额(元)的范围 |
[200,400] |
[400,500) |
[500,700] |
[700,900] |
… |
|
获得奖券的金额(元) |
30 |
60 |
100 |
130 |
… |
根据上述促销方法,顾客在该商场购物可以获得双重优惠.例如,购买标价为400元的商品,则消费金额为320元,获得的优惠额为:400×0.2+30=110(元).设购买商品得到的优惠率=![]() .试问:
.试问:
(1)若购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)对于标价在[500,800](元)内的商品,顾客购买标价为多少元的商品,可得到不小于![]() 的优惠率?
的优惠率?
查看习题详情和答案>>
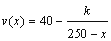 ,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时.
,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时. 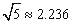 )
)