摘要:若a,b∈R,求证:≤+. 证明 当|a+b|=0时.不等式显然成立. 当|a+b|≠0时.由0<|a+b|≤|a|+|b|≥, 所以=≤=≤+.
网址:http://m.1010jiajiao.com/timu_id_3966145[举报]
已知a>0,b∈R,函数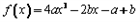 。
。
(Ⅰ)证明:当0≤x≤1时,
(i)函数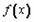 的最大值为|2a-b|﹢a;
的最大值为|2a-b|﹢a;
(ii) +|2a-b|﹢a≥0;
+|2a-b|﹢a≥0;
(Ⅱ)若-1≤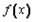 ≤1对x∈[0,1]恒成立,求a+b的取值范围。
≤1对x∈[0,1]恒成立,求a+b的取值范围。
查看习题详情和答案>>
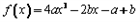 。
。(Ⅰ)证明:当0≤x≤1时,
(i)函数
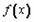 的最大值为|2a-b|﹢a;
的最大值为|2a-b|﹢a;(ii)
 +|2a-b|﹢a≥0;
+|2a-b|﹢a≥0;(Ⅱ)若-1≤
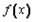 ≤1对x∈[0,1]恒成立,求a+b的取值范围。
≤1对x∈[0,1]恒成立,求a+b的取值范围。
已知a>0,b∈R,函数f(x)=4ax3-2bx-a+b.
(Ⅰ)证明:当0≤x≤1时,
(i)函数f(x)的最大值为|2a-b|+a;
(ii)f(x)+|2a-b|+a≥0;
(Ⅱ)若-1≤f(x)≤1对x∈[0,1]恒成立,求a+b的取值范围.
查看习题详情和答案>>
(Ⅰ)证明:当0≤x≤1时,
(i)函数f(x)的最大值为|2a-b|+a;
(ii)f(x)+|2a-b|+a≥0;
(Ⅱ)若-1≤f(x)≤1对x∈[0,1]恒成立,求a+b的取值范围.
查看习题详情和答案>>
(2012•浙江)已知a>0,b∈R,函数f(x)=4ax3-2bx-a+b.
(Ⅰ)证明:当0≤x≤1时,
(i)函数f(x)的最大值为|2a-b|+a;
(ii)f(x)+|2a-b|+a≥0;
(Ⅱ)若-1≤f(x)≤1对x∈[0,1]恒成立,求a+b的取值范围.
查看习题详情和答案>>
(Ⅰ)证明:当0≤x≤1时,
(i)函数f(x)的最大值为|2a-b|+a;
(ii)f(x)+|2a-b|+a≥0;
(Ⅱ)若-1≤f(x)≤1对x∈[0,1]恒成立,求a+b的取值范围.