摘要： 数学归纳法是一种证明方法.归纳推理是一种推理方法.
网址：http://m.1010jiajiao.com/timu_id_3965014[举报]
假设当n=k(k∈N*，k≥n0)时命题成立，并证明当n=k+1时，命题________.于是命题对一切n∈N*，n≥n0,都成立.这种证明方法叫做_________.?
运用数学归纳法证明命题要分两步走.第一步是递推的_________;第二步是递推的________，这两步是缺一不可的.
查看习题详情和答案>>
下列四种说法中正确的是 ．
①“若am2＜bm2，则a＜b”的逆命题为真；
②线性回归方程对应的直线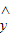
=
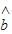x+
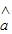一定经过其样本数据点 （x1，y1），（x2，y2），…，（xn，yn）中的一个点；
③若实数x，y∈[0，1]，则满足：x2+y2＞1的概率为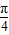
；
④用数学归纳法证明（n+1）（n+2）…（n+n）=2n•1•3…（2n-1）（n∈N*）时，从“k”到“k+1”的证明，左边需增添的一个因式是2（2k+1）． 查看习题详情和答案>>
①“若am2＜bm2，则a＜b”的逆命题为真；
②线性回归方程对应的直线
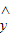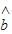=x+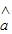一定经过其样本数据点 （x1，y1），（x2，y2），…，（xn，yn）中的一个点；③若实数x，y∈[0，1]，则满足：x2+y2＞1的概率为
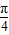；④用数学归纳法证明（n+1）（n+2）…（n+n）=2n•1•3…（2n-1）（n∈N*）时，从“k”到“k+1”的证明，左边需增添的一个因式是2（2k+1）． 查看习题详情和答案>>
下列四种说法中正确的是 ．
①“若am2＜bm2，则a＜b”的逆命题为真；
②线性回归方程对应的直线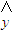
=
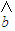x+
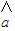一定经过其样本数据点 （x1，y1），（x2，y2），…，（xn，yn）中的一个点；
③若实数x，y∈[0，1]，则满足：x2+y2＞1的概率为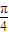
；
④用数学归纳法证明（n+1）（n+2）…（n+n）=2n•1•3…（2n-1）（n∈N*）时，从“k”到“k+1”的证明，左边需增添的一个因式是2（2k+1）． 查看习题详情和答案>>
①“若am2＜bm2，则a＜b”的逆命题为真；
②线性回归方程对应的直线
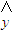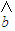=x+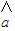一定经过其样本数据点 （x1，y1），（x2，y2），…，（xn，yn）中的一个点；③若实数x，y∈[0，1]，则满足：x2+y2＞1的概率为
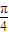；④用数学归纳法证明（n+1）（n+2）…（n+n）=2n•1•3…（2n-1）（n∈N*）时，从“k”到“k+1”的证明，左边需增添的一个因式是2（2k+1）． 查看习题详情和答案>>
=
x+
一定经过其样本数据点 （x1，y1），（x2，y2），…，（xn，yn）中的一个点；
；