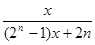摘要: 归纳推理:根据一类事物的部分对象具有某种性质.推出这类事物的所有对象都具有这种性质的推理.
网址:http://m.1010jiajiao.com/timu_id_3965000[举报]
 ∴当n=k+1时,不等式成立.
∴当n=k+1时,不等式成立.
根据(1)和(2)可知对任何![]() 都成立.则上述证法( )
都成立.则上述证法( )
A.过程全部正确
B.n=1验得不正确
C.归纳假设不正确
D.从n=k到n=k+1的推理不正确
查看习题详情和答案>>设函数f(x)=
(x>0),观察:f1(x)=f(x)=
,f2(x)=f(f1(x))=
,f3(x)=f(f2(x))=
,f4(x)=f(f3(x))=
…根据以上事实,由归纳推理可得当n∈N*且n≥2时,fn(x)=f(fn-1(x))=( )
| x |
| x+2 |
| x |
| x+2 |
| x |
| 3x+4 |
| x |
| 7x+8 |
| x |
| 15x+16 |
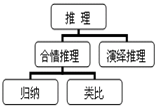 如图是《推理》知识结构框图,根据该框图可得
如图是《推理》知识结构框图,根据该框图可得 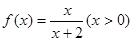 ,观察:
,观察: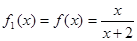 ,
,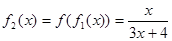 ,,
,, ,
, 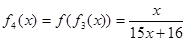 ……根据以上事实,由归纳推理可得当
……根据以上事实,由归纳推理可得当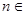 N*且
N*且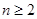 时,
时, 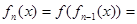 (
)
(
)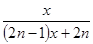 B.
B.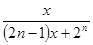 C.
C.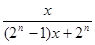 D.
D.