网址:http://m.1010jiajiao.com/timu_id_3964565[举报]
(2)太阳系只是银河系中一个非常渺小的角落,银河系中至少还有3000多亿颗恒星,银河系中心的质量相当于400万颗太阳的质量.通过观察发现,恒星绕银河系中心运动的规律与开普勒第三定律存在明显的差异,且周期的平方跟圆轨道半径的立方之比随半径的增大而减小.请你对上述现象发表看法.
(14分)
(1)开普勒行星运动第三定律指出:行星绕太阳运动的椭圆轨道的半长轴a的三次方与它的公转周期T的二次方成正比,即![]() ,k是一个对所有行星都相同的常量。将行星绕太阳的运动按圆周运动处理,请你推导出太阳系中该常量k的表达式。已知引力常量为G,太阳的质量为M太。
,k是一个对所有行星都相同的常量。将行星绕太阳的运动按圆周运动处理,请你推导出太阳系中该常量k的表达式。已知引力常量为G,太阳的质量为M太。
(2)开普勒定律不仅适用于太阳系,它对一切具有中心天体的引力系统(如地月系统)都成立。经测定月地距离为3.84×108m,月球绕地球运动的周期为2.36×106S,试计算地球的质M地。(G=6.67×10-11Nm2/kg2,结果保留一位有效数字)
【解析】:(1)因行星绕太阳作匀速圆周运动,于是轨道的半长轴a即为轨道半径r。根据万有引力定律和牛顿第二定律有
![]() ①
①
于是有 ![]() ②
②
即 ![]() ③
③
(2)在月地系统中,设月球绕地球运动的轨道半径为R,周期为T,由②式可得
![]() ④
④
解得 M地=6×1024kg ⑤
(M地=5×1024kg也算对)
23.【题文】(16分)
 如图所示,在以坐标原点O为圆心、半径为R的半圆形区域内,有相互垂直的匀强电场和匀强磁场,磁感应强度为B,磁场方向垂直于xOy平面向里。一带正电的粒子(不计重力)从O点沿y轴正方向以某一速度射入,带电粒子恰好做匀速直线运动,经t0时间从P点射出。
如图所示,在以坐标原点O为圆心、半径为R的半圆形区域内,有相互垂直的匀强电场和匀强磁场,磁感应强度为B,磁场方向垂直于xOy平面向里。一带正电的粒子(不计重力)从O点沿y轴正方向以某一速度射入,带电粒子恰好做匀速直线运动,经t0时间从P点射出。
(1)求电场强度的大小和方向。
(2)若仅撤去磁场,带电粒子仍从O点以相同的速度射入,经![]() 时间恰从半圆形区域的边界射出。求粒子运动加速度的大小。
时间恰从半圆形区域的边界射出。求粒子运动加速度的大小。
(3)若仅撤去电场,带电粒子仍从O点射入,且速度为原来的4倍,求粒子在磁场中运动的时间。
查看习题详情和答案>>
 (1)一物体静止在水平面上,它的质量是m,与水平面之间的动摩擦因数为μ.用平行于水平面的力F分别拉物体,得到加速度a和拉力F的关系图象如图所示.利用图象可求出这个物体的质量m.
(1)一物体静止在水平面上,它的质量是m,与水平面之间的动摩擦因数为μ.用平行于水平面的力F分别拉物体,得到加速度a和拉力F的关系图象如图所示.利用图象可求出这个物体的质量m.甲同学分析的过程是:从图象中得到F=12N时,物体的加速度a=4m/s2,根据牛顿定律导出:m=
| F |
| a |
乙同学的分析过程是:从图象中得出直线的斜率为:k=tan45°=1,而K=
| 1 |
| m |
请判断甲、乙两个同学结论的对和错,并分析错误的原因.如果两个同学都错,分析各自的错误原因后再计算正确的结果.
(2)两颗靠得很近的天体,离其他天体非常遥远,靠相互吸引力一起以连线上某一点为圆心分别作圆周运动,从而保持两者之间的距离不变,这样的天体称为“双星’.现测得两星中心间距离为R,运动周期为T,求:双星的总质量.
解:设双星的质量分别为M1、M2.它们绕其连线上的O点以周期T作匀速圆周运动,由万有引力定律及牛顿第二定律得:G
| M1M2 |
| R2 |
| 2π |
| T |
| M1M2 |
| R2 |
| 2π |
| T |
请判断上述解法是否正确,若正确,请完成计算;若不正确,请说明理由,并用你自己的方法算出正确结果.
 (1)一物体静止在水平面上,它的质量是m,与水平面之间的动摩擦因数为μ.用平行于水平面的力F分别拉物体,得到加速度a和拉力F的关系图象如图所示.利用图象可求出这个物体的质量m.
(1)一物体静止在水平面上,它的质量是m,与水平面之间的动摩擦因数为μ.用平行于水平面的力F分别拉物体,得到加速度a和拉力F的关系图象如图所示.利用图象可求出这个物体的质量m.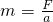 得:m=3kg
得:m=3kg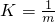 ,所以m=1kg
,所以m=1kg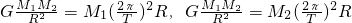 联立解得:M1+M2=…
联立解得:M1+M2=…