摘要： 证明:. 又.. ． ．
网址：http://m.1010jiajiao.com/timu_id_3961167[举报]
（1）证明：∵
，
∴
． …………………………………………（2分）
∵
， …………………………………………（1分）
∴
∽
．……………………………………… （1分）
∴
． ……………………………………………（1分）
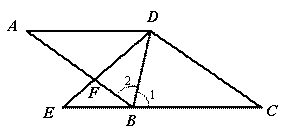
（2） ∵，
又∵
，
∴
．………………………………………………（1分）
∴
． ………………………………………………（1分）
又∵
，
∴四边形
是平行四边形 ………………………………………（1分）
∵，
∴
． ……………………………………………（1分）
∵
平分
，
∴
． …………………………………………（1分）
∴
．
∴
． ……………………………………………（1分）
∴四边形是菱形． ……………………………………………………（1分）
填写证明的理由．
已知：如图，AB∥CD，EF、CG分别是∠AEC、∠ECD的角平分线；求证：EF∥CG．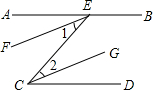
证明：∵AB∥CD（已知）
∴∠AEC=∠DCE （ ）
又∵EF平分∠AEC （已知）
∴∠1=
∠AEC （ ）
同理∠2=
∠DCE，∴∠1=∠2
∴EF∥CG （ ）
查看习题详情和答案>>
已知：如图，AB∥CD，EF、CG分别是∠AEC、∠ECD的角平分线；求证：EF∥CG．
证明：∵AB∥CD（已知）
∴∠AEC=∠DCE （
又∵EF平分∠AEC （已知）
∴∠1=
| 1 |
| 2 |
同理∠2=
| 1 |
| 2 |
∴EF∥CG （
实验证明，平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等．（1）如图，一束光线m射到平面镜a上，被a反射到平面镜b上，又被b反射．若被b反射出的光线n与光线m平行，且∠1=38°，则∠2=
76
76
°，∠3=90
90
°．（2）在（1）中，若∠1=55°，则∠3=
90
90
°；若∠1=40°，则∠3=90
90
°．（3）由（1）、（2），请你猜想：当两平面镜a、b的夹角∠3=
90
90
°时，可以使任何射到平面镜a上的光线m，经过平面镜a、b的两次反射后，入射光线m与反射光线n平行．你能说明理由吗？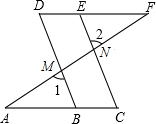
补全证明过程：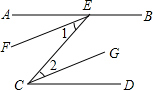
∠AEC （________）