摘要：证明:(1)在和中． (2).．又.．

网址：http://m.1010jiajiao.com/timu_id_3961160[举报]

22、完成下列证明：
（1）如图，已知AD⊥BC，EF⊥BC，∠1=∠2．求证：DG∥BA．
证明：∵AD⊥BC，EF⊥BC（已知）
∴∠EFB=∠ADB=90°

同位角相等，两直线平行

两直线平行，同位角相等

又∵∠1=∠2（已知）
∴

（等量代换）
∴DG∥BA

内错角相等，两直线平行

（2）如图，已知AB=AD，AC=AE，∠1=∠2，请说明BC=DE的理由．

解：∵∠1=∠2
∴∠1+

即∠BAC=∠DAE
在△ABC和△ADE中
AB=

（已知）
∠BAC=∠DAE（已证）

=AE（已知）
∴△ABC≌△ADE（

）
∴BC=DE（

全等三角形的对应边相等

查看习题详情和答案>>

在下列证明中添加需要补充的条件或理由．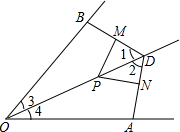

证明：∵OD平分∠AOB（已知）
∴∠

）
在△OBD和△OAD中，

OB=OA
∠3=∠4

∴△OBD≌△OAD（

）∴∠1=∠2
又∵PM⊥DB，PN⊥DA
∴

）查看习题详情和答案>>

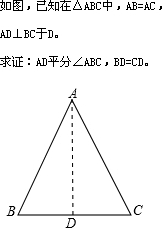小明在证明“等腰三角形底边上的高线、底边上的中线和顶角的平分线互相重合”这一命题时，画出图形，写出“已知”、“求证”（如图）．
（1）请你帮助小明完成证明过程．
（2）请你作出判断：小明写出的“已知”、“求证”是否完整？在横线上填“是”或“否”．
（3）做完（1）后，小明模仿老师上课时的方法，又提出了如下几个问题：
如：①若将题中“AD⊥BC”与“AD平分∠ABC”的位置交换，得到的是否仍是真命题？
②若将题中“AD⊥BC”与“BD=CD”的位置交换，得到的是否仍是真命题？请你作出判断，在下列横线上填写“是”或“否”：① ②__ 并对②的判断作出证明．（若是则写出证明过程；若不是则举出一个反例）

查看习题详情和答案>>

完成下列证明：
（1）如图，已知AD⊥BC，EF⊥BC，∠1=∠2．求证：DG∥BA．
证明：∵AD⊥BC，EF⊥BC（已知）
∴∠EFB=∠ADB=90°
∴EF∥AD
∴∠1=∠BAD
又∵∠1=∠2（已知）
∴（等量代换）
∴DG∥BA

（2）如图，已知AB=AD，AC=AE，∠1=∠2，请说明BC=DE的理由．
解：∵∠1=∠2
∴∠1+=∠2+
即∠BAC=∠DAE
在△ABC和△ADE中
AB=（已知）
∠BAC=∠DAE（已证）
=AE（已知）
∴△ABC≌△ADE（）
∴BC=DE（）

查看习题详情和答案>>

完成下列证明：
（1）如图，已知AD⊥BC，EF⊥BC，∠1=∠2．求证：DG∥BA．
证明：∵AD⊥BC，EF⊥BC（已知）
∴∠EFB=∠ADB=90°______
∴EF∥AD______
∴∠1=∠BAD______
又∵∠1=∠2（已知）
∴______（等量代换）
∴DG∥BA______

（2）如图，已知AB=AD，AC=AE，∠1=∠2，请说明BC=DE的理由

．
∵∠1=∠2
∴∠1+______=∠2+____________
即∠BAC=∠DAE
在△ABC和△ADE中
AB=______（已知）
∠BAC=∠DAE（已证）
______=AE（已知）
∴△ABC≌△ADE（______）
∴BC=DE（______）

查看习题详情和答案>>