摘要: 证明:连结AB 在△ADB与△ACB中∴△ADB≌△ACB∴OC=OD.
网址:http://m.1010jiajiao.com/timu_id_3961149[举报]
如图,AC、BD交于点E,AD=BC,∠C=∠D,求证:AC=BD.
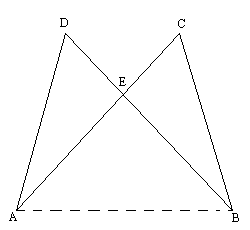
证明:连结AB
在△ABD和△BAC中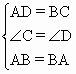
∴△ABD≌△BAC,∴AC=BD.
回答下列问题:
①上述证明过程是否有错,若有错,指出错在什么地方?并写出正确的证明过程.
③上述证明过程,充分说明,证明两个三角形全等,不能用________这个假命题,也就是说________两三角形不一定全等.
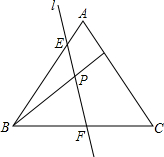 如图,在等边△ABC中,点D为AC上一点,连结AB,BD,BC分别相交于点E,P,F,且∠BPF=60°
如图,在等边△ABC中,点D为AC上一点,连结AB,BD,BC分别相交于点E,P,F,且∠BPF=60°(1)写出图中所有与△BPF相似的三角形,并选择其中一对给予证明;
(2)探究:当BD什么条件时(其它条件不变),PF=
| 1 | 2 |
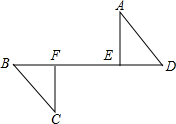 先填写完成第(1)小题中的空缺部分(数学表达式或理由),再按要求解答第(2)小题.
先填写完成第(1)小题中的空缺部分(数学表达式或理由),再按要求解答第(2)小题.如图:AD=CB,AE⊥BD,CF⊥BD,垂足分别是E、F,DF=BE.
(1)求证:∠D=∠B;
(2)请你连结AB、CD,探究AB与CD有何位置关系?并证明你的结论.
证明:(1)∵AE⊥BD,CF⊥BD,
∴∠AED=∠
CFB
CFB
=90°,∵DF=BE,
∴DF-
EF
EF
=BE-EF
EF
,即DE=BF.
在Rt△ADE和Rt△CBF中,
方程组:
∴Rt△ADE≌Rt△CBF
HL
HL
,∴∠D=∠B
全等三角形的对应角相等
全等三角形的对应角相等
.(2)
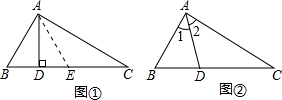 我们知道,利用三角形全等可以证明两条线段相等.但是我们会碰到这样的“和差”问题:“如图①,AD为△ABC的高,∠ABC=2∠C,证明:CD=AB+BD”.我们可以用“截长、补短”的方法将这类问题转化为证明两条线段相等的问题:在CD上截取DE=BD,连结AE.
我们知道,利用三角形全等可以证明两条线段相等.但是我们会碰到这样的“和差”问题:“如图①,AD为△ABC的高,∠ABC=2∠C,证明:CD=AB+BD”.我们可以用“截长、补短”的方法将这类问题转化为证明两条线段相等的问题:在CD上截取DE=BD,连结AE.(1)请补写完这个证明:
(2)运用上述方法证明:如图②,AD平分∠BAC,∠ABC=2∠C,证明:BD=AC-AB.
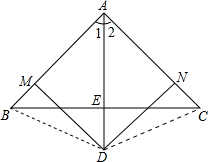 多彩数学,所有三角形都是等腰三角形
多彩数学,所有三角形都是等腰三角形下面的推理过程,请你指出其错误之处.如图:△ABC中,∠BAC的平分线和BC边的垂直平分线相交于D,过点D作DM⊥AB于M,DN⊥AC于N.求证:AB=AC.
证明:连结BD、CD.
∵DM⊥AB,∴∠DMA=90°.∵DN⊥AC,∴∠AND=90°.∴∠AMD=∠AND=90°.又AD平分∠BAC,∴∠1=∠2.又∵AD=AD,∵△ADM≌△ADN(AAS),∴AM=AN,DM=DN.∵DE垂直平分BC,∴DB=DC.在Rt△BDM与Rt△CDN中,
|
分三种情况:
(1)AB=AC时成立;
(2)AB>AC时,N在AC的延长线上;
(3)AB<AC时,M在AB的延长线上.