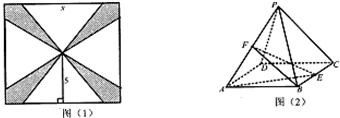
摘要:15.如下的三个图.分别是一个长方体截去一个角所得多面体的直观图以及它的正视图和侧视图 (1)按照画三视图的要求画出该多面体的俯视图, (2)按照给出的尺寸.求该多面体的体积, (3)在所给直观图中连结.证明:面.
网址:http://m.1010jiajiao.com/timu_id_3953732[举报]
 求答下列三小题:
求答下列三小题:(1)在棱长为1的正方体上,分别用过共顶点的三条棱中点的平面截该正方形,
则截去8个三棱锥后,剩下的几何体的体积是多少?
(2)圆锥的轴截面是等腰直角三角形,侧面积是16
| 2 |
(3)一简单组合体的三视图及尺寸如图所示(单位:cm),求该组合体的表面积.
在边长为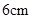 的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥.
的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥.
(I)判别MN与平面AEF的位置关系,并给出证明;
(II)求多面体E-AFMN的体积.


【解析】第一问因翻折后B、C、D重合(如下图),所以MN应是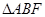 的一条中位线,则利用线线平行得到线面平行。
的一条中位线,则利用线线平行得到线面平行。
第二问因为 平面BEF,……………8分
平面BEF,……………8分
且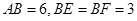 ,
,
∴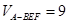 ,又
,又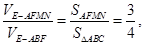 ∴
∴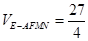
(1)因翻折后B、C、D重合(如图),

所以MN应是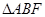 的一条中位线,………………3分
的一条中位线,………………3分
则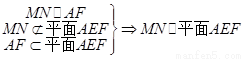 .………6分
.………6分
(2)因为 平面BEF,……………8分
平面BEF,……………8分
且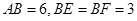 ,
,
∴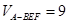 ,………………………………………10分
,………………………………………10分
又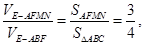 ∴
∴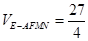
查看习题详情和答案>>
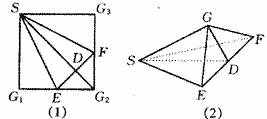
在边长为1的正方形SG1G2G3中,E,F分别是G1G2及G2G3的中点,D是EF的中点,现在沿SE,SF及EF把这个正方形折成一个由四个三角形围成的“四面体”,使G1,G2,G3三点重合,重合后的点记为G(如下图),那么在四面体S-EFG外接球的半径是
A.![]() B.
B.![]() C.
C.![]() D.以上都不对
D.以上都不对