摘要:当n∈N*时.证明: 如图.已知四棱锥的底面是菱形, 平面, 点为的中点. (1)求证:平面, (2)求证:平面, (3)若PA=AB=2.∠ABC=60o.求二面角P-BC-A的大小. 设函数...且以为最小正周期. (1)求, (2)求的解析式, (3)已知.求的值. 设是不等式的解集.整数. (1)记使得“成立的有序数组 为事件A.试列举A包含的基本事件, (2)设.求的分布列及其数学期望. 已知等差数列满足:..的前项和为 (Ⅰ)求及, (Ⅱ)令().求数列的前项和为 已知中心在坐标原点O的椭圆C经过点A为其右焦点. (1)求椭圆C的方程, (2)是否存在平行于OA的直线.使得直线与椭圆C有公共点.且直线OA与的距离等于4?若存在.求出直线的方程,若不存在.请说明理由.
网址:http://m.1010jiajiao.com/timu_id_3946656[举报]
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
(17)(本小题满分12分)
已知函数 .
.
(I)求函数 的最小正周期;
的最小正周期;
(Ⅱ)当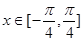 时,函数
时,函数 的最小值为
的最小值为 ,求实数
,求实数 的值.
的值.
查看习题详情和答案>>
((本小题满分12分)
编号分别为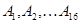 的16名篮球运动员在某次比赛中得分记录如下;
的16名篮球运动员在某次比赛中得分记录如下;
|
编号 |
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
A8 |
|
得分 |
15 |
35 |
21 |
28 |
25 |
36 |
18 |
34 |
|
编号 |
A9 |
A10 |
A11 |
A12 |
A13 |
A14 |
A15 |
A16 |
|
得分 |
17 |
26 |
25 |
33 |
22 |
12 |
31 |
38 |
(Ⅰ)将得分在对应区间的人数填入相应的空格内:
|
区 间 |
|
|
|
|
人 数 |
|
|
|
(Ⅱ)从得分在区间 内的运动员中随机抽取2人.
内的运动员中随机抽取2人.
(1)用运动员编号列出所有可能的抽取结果;
(2)求这两人得分之和大于50的概率.
查看习题详情和答案>>
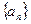 中,
中,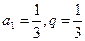 ,
,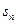 为数列
为数列 项的和,证明:
项的和,证明:
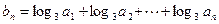 ,求数列
,求数列 的通项公式;
的通项公式;