摘要：已知关于x的二次函数f(x)＝x2+(2t-1)x+1-2t. (1)求证:对于任意t∈R.方程f(x)＝1必有实数根, (2)若＜t＜.求证:方程f(x)＝0在区间内各有一个实数根. 解:(1)证明:由f(1)＝1知f(x)＝1必有实数根. (2)当＜t＜时.因为f(-1)＝3-4t＝4(-t)＞0. f(0)＝1-2t＝2(-t)＜0. f()＝+(2t-1)+1-2t＝-t＞0. 所以方程f(x)＝0在区间内各有一个实数根.
网址：http://m.1010jiajiao.com/timu_id_3946487[举报]
已知关于x的二次函数f（x）=ax2-4bx+1
（Ⅰ）设集合P={1，2，3}，集合Q={-1，1，2，3，4}，从集合P中随机取一个数作为a，从集合Q中随机取一个数作为b，求函数f（x）在区间[1，+∞）上是增函数的概率；
（Ⅱ）设点（a，b）是区域
内的随机点，求函数f（x）在区间[1，+∞）上是增函数的概率．
查看习题详情和答案>>
（Ⅰ）设集合P={1，2，3}，集合Q={-1，1，2，3，4}，从集合P中随机取一个数作为a，从集合Q中随机取一个数作为b，求函数f（x）在区间[1，+∞）上是增函数的概率；
（Ⅱ）设点（a，b）是区域
|
已知关于x的二次函数f（x）=x2+（2t-1）x+1-2t．
（1）求证：对于任意t∈R，方程f（x）=1必有实数根；
（2）若方程f（x）=0在区间（-1，2）上有两个实数根，求t的范围． 查看习题详情和答案>>
（1）求证：对于任意t∈R，方程f（x）=1必有实数根；
（2）若方程f（x）=0在区间（-1，2）上有两个实数根，求t的范围． 查看习题详情和答案>>
已知关于x的二次函数f（x）=ax2-2bx-1，（其中常数a、b∈R），满足
，则函数y=f（x）在区间[2，+∞）上是增函数的概率是（ ）
|
A、
| ||
B、
| ||
C、
| ||
D、
|
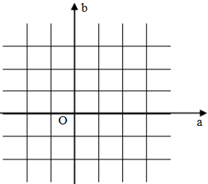已知关于x的二次函数f（x）=x2+ax-b（a，b∈R）．