摘要：设奇函数f(x)在 [-1,1]上是增函数.f(-1)＝-1.若函数f(x)≤t2-2at+1对所有的x∈[-1,1]都成立.则当a∈[-1,1]时.t的取值范围是 . 解析:若函数f(x)≤t2-2at+1对所有的x∈[-1,1]都成立.由已知易得f(x)的最大值是1. ∴1≤t2-2at+1⇔2at-t2≤0. 设g(a)＝2at-t2(-1≤a≤1).欲使2at-t2≤0恒成立. 则⇔t≥2或t＝0或t≤-2. 答案:t≤-2或t＝0或t≥2 题组四 函数单调性的综合应用
网址：http://m.1010jiajiao.com/timu_id_3946414[举报]
设奇函数f(x)在[－1,1]上是增函数，且f(－1)＝－1，若函数f(x)≤t2－2at＋1对所有的x∈[－1,1]都成立，则当a∈[－1,1]时t的取值范围是( )．
A．－2≤t≤2 B．－
≤t≤
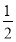
C．t≤－2或t＝0或t≥2 D．t≤－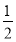
或t＝0或t≥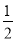
查看习题详情和答案>>
设奇函数f(x)在[－1,1]上是增函数，且f(－1)＝－1，若函数f(x)≤t2－2at＋1对所有的x∈[－1,1]都成立，则当a∈[－1,1]时t的取值范围是( )．
| A．－2≤t≤2 | B．－ ≤t≤ |
| C．t≤－2或t＝0或t≥2 | D．t≤－或t＝0或t≥ |
设奇函数f(x)在[－1，1]上是增函数，且f(－1)＝－1．若函数，f(x)≤t2－2at＋1对所有的x∈[－1．1]都成立，则当a∈[1，1]时，t的取值范围是
[ ]
A．－2≤t≤2
B．
≤t≤
C．
t≤－2或t＝0或t≥2
D．
t≤
或t＝0或t≥
或
t＝0或
≤t≤