摘要：4．设函数f(x)＝x3+ax2-9x-1(a<0)．若曲线y＝f(x)的斜率最小的切线与直线12x+y＝6平行.求: (1)a的值, (2)函数f(x)的单调区间． 解:(1)因f(x)＝x3+ax2-9x-1. 所以f′(x)＝3x2+2ax-9 ＝32-9-. 即当x＝-时.f′(x)取得最小值-9-. 因斜率最小的切线与12x+y＝6平行.即该切线的斜率为-12.所以-9-＝-12.即a2＝9. 解得a＝±3.由题设a<0.所以a＝-3. 知a＝-3.因此f(x)＝x3-3x2-9x-1. f′(x)＝3x2-6x-9＝3(x-3)(x+1). 令f′(x)＝0.解得x1＝-1.x2＝3. 当x∈时.f′(x)>0. 故f(x)在上为增函数, 当x∈时.f′(x)<0. 故f(x)在上为减函数, 当x∈时.f′(x)>0.故f(x)在上为增函数． 由此可见.函数f(x)的单调递增区间为.单调递减区间为． 题组二 导数与函数的极值和最值
网址：http://m.1010jiajiao.com/timu_id_3946362[举报]
已知实数a满足1＜a≤2，设函数f (x)＝
x3－
x2＋a x．
(Ⅰ) 当a＝2时，求f (x)的极小值；
(Ⅱ) 若函数g(x)＝4x3＋3bx2－6(b＋2)x (b∈R) 的极小值点与f (x)的极小值点相同，
求证：g(x)的极大值小于或等于10．
查看习题详情和答案>>
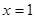处的切线方程为12x＋y－1＝0．
上的最大值和最小值．