摘要：数列{an}满足 a1=1,a2=2,. (1)求a3,a4,a5,a6; (2)设,Sn=b1+b2+-+bn,求Sn; 的条件下,证明当n≥6时,. (1)解:因为a1=1,a2=2,所以, a4=(2-|sinπ|)a2+|sinπ|=2a2=4, 同理a5=3,a6=8. (2)解:因为, 即a2n+1-a2n-1=1. 所以数列{a2n-1}是首项为1,公差为1的等差数列,因此a2n-1=n. 又因为, 所以数列{a2n}是首项为2,公比为2的等比数列,因此a2n=2n. 所以,. ,① .② 由①-②,得. 所以. (3)证明:要证明当n≥6时,成立,只需证明当n≥6时,成立. 证法一:①当n=6时,成立. ②假设当n=k(k≥6)时不等式成立,即. 则当n=k+1时, . 由①②所述,当n≥6时,,即当n≥6时,. 证法二:令(n≥6),则. 所以当n≥6时,cn+1＜cn. 因此当n≥6时,. 于是当n≥6时,. 综上所述,当n≥6时,.
网址：http://m.1010jiajiao.com/timu_id_3942866[举报]
（本小题满分15分）已知等差数列{an}中，首项a1＝1，公差d为整数，且满足a1+3＜a3，a2+5＞a4，数列{bn}满足
，其前n项和为Sn．（1）求数列{an}的通项公式an；（2）若S2为S1，Sm(m∈N*)的等比中项，求正整数m的值．
（本小题满分15分）已知等差数列{an}中，首项a1＝1，公差d为整数，且满足a1+3＜a3，a2+5＞a4，数列{bn}满足
，其前n项和为Sn．（1）求数列{an}的通项公式an；（2）若S2为S1，Sm(m∈N*)的等比中项，求正整数m的值．
（本小题满分15分）
已知等差数列{an}中，首项a1＝1，公差d为整数，且满足a1+3＜a3，a2+5＞a4，数列{bn}满足
，其前n项和为Sn．
（1）求数列{an}的通项公式an；
（2）若S2为S1，Sm(m∈N*)的等比中项，求正整数m的值．
查看习题详情和答案>>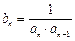
，其前n项和为Sn．
，其前n项和为Sn．（1）求数列{an}的通项公式an；（2）若S2为S1，Sm(m∈N*)的等比中项，求正整数m的值．