摘要： 已知数列满足:(n∈N*) (Ⅰ)求证:数列为等差数列, (Ⅱ)求数列的能项公式, (Ⅲ)求下表中前n行所有数的和. -- - -- 解:(Ⅰ)由条件a1＝1... 得 ∴数列为等差数列． 得 ∴ ＝2×3×-×n＝n! ∴ (Ⅲ)∵(k＝1.2.-.n) ∴第n行各数之和(n＝1.2.-) ∴表中前n行所有数的和 Sn＝(22-2)+(23-2)+-+(2n+1-2) ＝(22+23+-+2n+1)-2n ＝2n+2-2n-4．
网址：http://m.1010jiajiao.com/timu_id_3942865[举报]
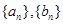满足：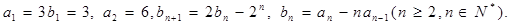
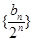是等差数列还是等比数列，并由此求数列
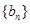的通项公式；
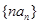的前n项和
(本小题满分14分)
已知数列{an}和{bn}满足：a1=λ，an+1=
其中λ为实数，n为正整数。
（Ⅰ）对任意实数λ，证明数列{an}不是等比数列；
（Ⅱ）试判断数列{bn}是否为等比数列，并证明你的结论；
（Ⅲ）设0＜a＜b，Sn为数列{bn}的前n项和。是否存在实数λ，使得对任意正整数n，都有
a＜Sn＜b?若存在，求λ的取值范围；若不存在，说明理由。
查看习题详情和答案>>(本小题满分14分)
已知数列{an}和{bn}满足：a1=λ，an+1=
其中λ为实数，n为正整数。
（Ⅰ）对任意实数λ，证明数列{an}不是等比数列；
（Ⅱ）试判断数列{bn}是否为等比数列，并证明你的结论；
（Ⅲ）设0＜a＜b，Sn为数列{bn}的前n项和。是否存在实数λ，使得对任意正整数n，都有
a＜Sn＜b?若存在，求λ的取值范围；若不存在，说明理由。
查看习题详情和答案>>
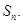
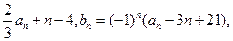其中λ为实数，n为正整数。
其中λ为实数，n为正整数。