摘要:已知数列的相邻两项.是关于x的方程(n∈N*)的根.且. (Ⅰ)求数列和的通项公式, (Ⅱ)设是数列的前n项和.问是否存在常数λ.使得对任意n∈N*都成立.若存在.求出λ的取值范围,若不存在.请说理理由. 解:本小题主要考查数列的通项公式.数列前n项和.不等式等基础知识.考查化归与转化.分类与整合.特殊与一般的数学思想方法.以及推理论证能力.运算求解能力和抽象概括能力. (Ⅰ)∵an.an+l是关于x的方程x2-2nx+bn=0(n∈N*)的两根. ∴. 求数列{ an}的通项公式.给出如下四种解法: 解法1:由an+an+l=2n.得 . 故数列是首项为.公比为-1的等比数列. ∴.即. 解法2:由an+an+l=2n.两边同除以(-1)n+1. 得. 令.则cn+1-cn=-(-2)n. 故cn = c1+(c2- c1)+(c3-c2)+-+(cn-cn-1) =-1-2-(-2)3---(-2)n-1 (n ≥ 2). 且也适合上式. ∴(n∈N*). ∴.即. 解法3:由an+an+l=2n.得an+1+an+2=2n+1. 两式相减得an+2-an=2n+1-2n=2n. 当n为正奇敬时. an=a1+(a3-a1)+(a5-a3)+-+(an-an-2) =1+2+23+25+-+2n-2 (n ≥ 3). 且a1=1也适合上式. 当n为正偶数时. an=a2+(a4- a2)+(a6- a4)+-+(an- an-2) =1+22+24+26+-+2n-2 (n ≥ 4). 且a2=21-a1=1也适合上式. ∴当n∈N*时. 解法4:由an+an+l=2n.a1=1. 得. . 猜想. 下面用数学归纳法证明猜想正确. ①当n=1时.易知猜想成立, ②假设当n=k(k=N*)时.猜想成立. 即. 由ak+ak+l=2k. 得. 故当n=k+1时.猜想也成立. 由①②得.对任意n∈N*.. ∴ . (Ⅱ)Sn=a1+ a2+ a3+-+an . 要使bn-λ Sn>0对任意n∈N*都成立. 即(*)对任意n∈N*都成立. ①当n为正奇数时.由(*)式得 . 即. ∵2n+1-1>0. ∴对任意正奇数n都成立. 当且仅当n=1时.有最小值1. ∴λ<1. ②当n为正偶数时.由(*)式得 . 即. ∵2n-1>0. ∴对任意正偶数n都成立. 当且仅当n=2时.有最小值. ∴. 综上所述.存在常数λ.使得bn-λ Sn>0对任意n∈N*都成立.λ的取值范围是
网址:http://m.1010jiajiao.com/timu_id_3942864[举报]
.(本小题满分14分)
已知数列 的相邻两项
的相邻两项 是关于
是关于 的方程
的方程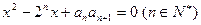 的两实根,且
的两实根,且 ,记数列
,记数列 的前
的前 项和为
项和为 .
.
(1)求 ;
;
(2)求证:数列 是等比数列;
是等比数列;
(3) 设
设 ,问是否存在常数
,问是否存在常数 ,使得
,使得 对
对 都成立,若存在,
都成立,若存在,
求出 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
.(本小题满分14分)
已知数列 ,
, ,其中
,其中 是方程
是方程 的两个根.
的两个根.
(1)证明:对任意正整数 ,都有
,都有 ;
;
(2)若数列 中的项都是正整数,试证明:任意相邻两项的最大公约数均为1;
中的项都是正整数,试证明:任意相邻两项的最大公约数均为1;
(3)若 ,证明:
,证明: 。
。
查看习题详情和答案>>
 ,
, 的相邻两项
的相邻两项 是关于
是关于 的方程
的方程 的两实根,且
的两实根,且 ,记数列
,记数列 项和为
项和为 .
. ;
; 是等比数列;
是等比数列; ,问是否存在常数
,问是否存在常数 ,使得
,使得 对
对 都成立,若存在,
都成立,若存在,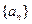 的相邻两项
的相邻两项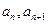 是关于
是关于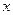 的方程
的方程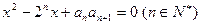 的两实根,且
的两实根,且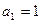 ,记数列
,记数列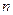 项和为
项和为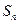 .
.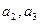 ;
;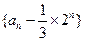 是等比数列;
是等比数列; 设
设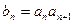 ,问是否存在常数
,问是否存在常数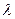 ,使得
,使得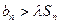 对
对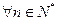 都成立,若存在,
都成立,若存在,