摘要： 已知.椭圆C过点A.两个焦点为. (1) 求椭圆C的方程, (2) E,F是椭圆C上的两个动点.如果直线AE的斜率与AF的斜率互为相反数.证明直线EF的斜率为定值.并求出这个定值. 解: (Ⅰ)由题意.c=1,可设椭圆方程为.解得. 所以椭圆方程为. -----4分 (Ⅱ)设直线AE方程为:.代入得 设,,因为点在椭圆上.所以 ---8分 又直线AF的斜率与AE的斜率互为相反数.在上式中以-K代K.可得 所以直线EF的斜率 即直线EF的斜率为定值.其值为. --12分
网址：http://m.1010jiajiao.com/timu_id_3938381[举报]
（2009辽宁卷理）（本小题满分12分）
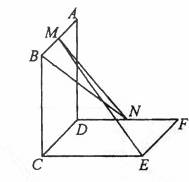
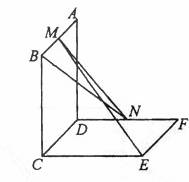
如图，已知两个正方行ABCD 和DCEF不在同一平面内，M，N分别为AB，DF的中点 。
（I）若平面ABCD ⊥平面DCEF，求直线MN与平面DCEF所成角的正值弦；
（II）用反证法证明：直线ME 与 BN 是两条异面直线。
，两个焦点为（－1，0），（1，0）。