（本小题满分12分）

阅读下面内容，思考后做两道小题。

在一节数学课上，老师给出一道题，让同学们先解，题目是这样的：

已知函数f(x)=kx+b，1≤f(1)≤3，－1≤f(－1)≤1，求Z=f(2)的取值范围。

题目给出后，同学们马上投入紧张的解答中，结果很快出来了，大家解出的结果有很多个，下面是其中甲、乙两个同学的解法：

甲同学的解法：由f(1)=k+b，f(－1)=－k+b得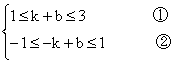

①+②得：0≤2b≤4，即0≤b≤2               ③

② ×(－1)+①得：－1≤k－b≤1             ④

④+②得：0≤2k≤4                                               ⑤

③+⑤得：0≤2k+b≤6。

又∵f(2)=2k+b

∴0≤f(2)≤6，0≤Z≤6

      乙同学的解法是：由f(1)=k+b，f(－1)=－k+b得

①+②得：0≤2b≤4，即：0≤b≤2                        ③

①－②得：2≤2k≤2，即：1≤k≤1

∴k=1，

∵f(2)=2k+b=1+b

由③得：1≤f(2)≤3

∴：1≤Z≤3

（Ⅰ）如果课堂上老师让你对甲、乙两同学的解法给以评价，你如何评价？

（Ⅱ）请你利用线性规划方面的知识，再写出一种解法。